题目内容
【题目】如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.
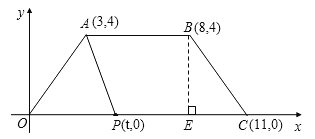
(1)过点B作BE⊥x轴于点E,则BE= ,用含t的代数式表示PC= .
(2)求S与t的函数关系.
(3)当S=20时,直接写出线段AB与CP的长.
【答案】(1)BE=4,PC=11-t;(2)S=-2t+32;(3)AB=PC=5.
【解析】
试题分析:(1)过点B作BE⊥X轴于点E,由B(8,4),即可求得BE=4,由于C(11,0),点P(t,0),于是得到OC=11,OP=t,即可得到结论;
(2)由梯形面积公式S=![]() (AB+PC)BE,代入数据即可得到结论;
(AB+PC)BE,代入数据即可得到结论;
(3)把S=20,代入S=﹣2t+32得,得出t=6,求出PC=11﹣t=5=AB即可.
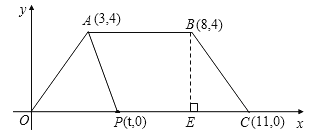
试题解析:(1)过点B作BE⊥x轴于点E,如图所示:
∵B(8,4),∴BE=4,∵C(11,0),点P(t,0),∴OC=11,OP=t,∴用含t的代数式表示PC=11﹣t;故答案为:4,11﹣t;
(2)由梯形的面积公式得:S=![]() (AB+PC)BE=
(AB+PC)BE=![]() (5+11﹣t)×4,∴S与t的函数关系为:S=﹣2t+32;
(5+11﹣t)×4,∴S与t的函数关系为:S=﹣2t+32;
(3)当S=20时,﹣2t+32=20,解得:t=6.此时,PC=11﹣t=5=AB.

练习册系列答案
相关题目