题目内容
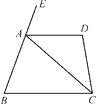
【题目】如图,![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上的中线,分别过点
上的中线,分别过点![]() ,
,![]() 作
作![]() ,
,![]()
的平行线交于点![]() ,且
,且![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,求
,求![]() 的值.
的值.

【答案】(1)证明过程见解析;(2)![]()
【解析】
试题分析:(1)、根据平行得出DBCE为平行四边形,根据CE=BD,CD是中线得出BD=AD,则CE=DA,结合CE∥DA得出ADCE为平行四边形,根据∠BCA=90°,CD为中线得出AD=CD,则四边形ADCE为菱形;(2)、作CF⊥AB,设BC=x,则AC=2x,根据Rt△ABC的勾股定理得出AB=![]() x,根据面积法得出CF的长度,然后进行计算sin∠CDB的值.
x,根据面积法得出CF的长度,然后进行计算sin∠CDB的值.
试题解析:(1)、∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 是平行四边形.∴
是平行四边形.∴![]() .
.
又∵![]() 是边
是边![]() 上的中线,∴
上的中线,∴![]() . ∴
. ∴![]() .又∵
.又∵![]() ,∴四边形
,∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,![]() 是斜边
是斜边![]() 上的中线,∴
上的中线,∴![]() .∴四边形
.∴四边形![]() 是菱形.
是菱形.
(2)、作![]() 于点
于点![]() .由(1) 可知,
.由(1) 可知, ![]() 设
设![]() ,则
,则![]() .
.
在![]() 中,根据勾股定理可求得
中,根据勾股定理可求得![]() .∵
.∵![]() ,
,
∴![]() ∵
∵![]() , ∴
, ∴![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目