题目内容
【题目】如图,已知直线y=x+3与 x轴、y轴交于A,B两点,直线![]() 经过原点,与线段AB交于点C,使△AOC的面积与△BOC的面积之比为2:1.
经过原点,与线段AB交于点C,使△AOC的面积与△BOC的面积之比为2:1.
(1)求A、B两点的坐标;
(2)求直线![]() 的函数解析式;
的函数解析式;
(3)在坐标平面是否存在点M,使得以A、C、O、M为顶点的四边形是平行四边形,若没有请说明理由,若有请直接写出M点的坐标.

【答案】(1)A(-3,0),B(0,3);(2)![]() (3)M1(-4,2),M2(2,2),M3(-2,-2)
(3)M1(-4,2),M2(2,2),M3(-2,-2)
【解析】(1)令y=0和x=0即可分别求出A、B两点坐标;
(2)根据△AOC的面积与△BOC的面积之比为2:1.可求出点C的坐标,再利用待定系数法即可求出直线![]() 的函数解析式;
的函数解析式;
(3)以AC、AO、CO三边分别为平行四边形的对角线即可得出点M的坐标.
解:(1)当y=0时,则x+3=0
解得,x=-3,
∴A(-3,0)
当x=0时,则y=0+3=3
∴B(0,3)
(2)设直线![]() 为
为![]()
∵A(-3,0) B(0,3)
∴S△AOB=![]()
∵S△AOC:S△BOC=2:1
∴S△AOC=![]() S△AOB=3
S△AOB=3
又∵AO=3
∴△AOC的AO边上的高为2,即C点的纵坐标为2
又∵C点在直线![]() 上
上
∴ C(-1,2)
又∵C点在直线![]() 上
上
∴直线![]() 为
为![]()
(3)存在点M,使得以A、C、O、M为顶点的四边形是平行四边形.
如图所示:
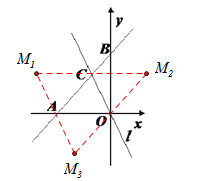
∴M1(-4,2),M2(2,2),M3(-2,-2)

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目

