题目内容
【题目】已知：如图，四边形ABCD中，AD∥BC，对角线AC、BD相交于点F，点E是边BC延长线上一点，且∠CDE=∠ABD，DB=DE。
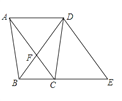
(1)求证：四边形ACED是平行四边形；
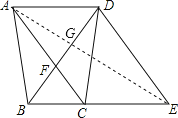
(2)联结AE，交BD于点G，求证: 
．
【答案】(1)证明见解析；（2）证明见解析.
【解析】分析：（1）证△ABD≌△CDE，推出AD=CE，由AD∥CE,即可推出结论；（2）根据平行得出比例式，再根据比例式的性质进行变形，即可得出答案．
本题解析：证明：(1)∵梯形ABCD,AD∥BC，AB=CD，
∴∠BAD=∠CDA，∵AD∥BE, ∴∠ADC=DCE, ∴∠DAB=DCE
在△BAD和△CDA中
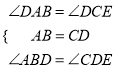
∴△ABD≌△CDE，∴AD=CE
又∵AD∥CE，∴∠ACD=∠CDE，
∴四边形ACED是平行四边形；
(2) ∵四边形ACED是平行四边形，∴FC∥DE, ∴
, ∵AD∥BE,
∴
,又∵AD=CE, ∴
练习册系列答案
相关题目
