题目内容
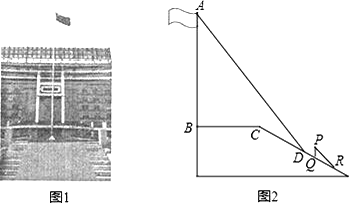
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
【答案】13.8.
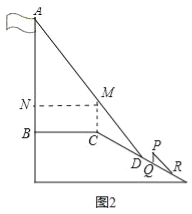
【解析】试题分析:如图,作CM∥AB交AD于M,MN⊥AB于N,根据![]() =
=![]() ,可求得CM的长,在RT△AMN中利用三角函数求得AN的长,再由MN∥BC,AB∥CM,判定四边形MNBC是平行四边形,即可得BN的长,最后根据AB=AN+BN即可求得AB的长.
,可求得CM的长,在RT△AMN中利用三角函数求得AN的长,再由MN∥BC,AB∥CM,判定四边形MNBC是平行四边形,即可得BN的长,最后根据AB=AN+BN即可求得AB的长.
试题解析:如图作CM∥AB交AD于M,MN⊥AB于N.
由题意![]() =
=![]() ,即
,即![]() =
=![]() ,CM=
,CM=![]() ,
,
在RT△AMN中,∵∠ANM=90°,MN=BC=4,∠AMN=72°,
∴tan72°=![]() ,
,
∴AN≈12.3,
∵MN∥BC,AB∥CM,
∴四边形MNBC是平行四边形,
∴BN=CM=![]() ,
,
∴AB=AN+BN=13.8米.

练习册系列答案
相关题目