题目内容
【题目】操作与实践:已知长方形纸片ABCD中,AD=3,AB=4.
操作一:如图①,任意画一条线段EF,将纸片沿EF折叠,使点B落到点B′的位置,EB′与CD交于点G.试说明重叠部分△EFG为等腰三角形;
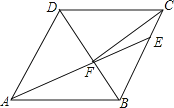
操作二:如图②,将纸片沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点H.求△B′HC的周长.

【答案】(1)证明见解析(2)7.
【解析】
试题分析:(1)由矩形的性质可知DC∥AB,根据平行线的性质可知∠GFE=∠FEB,由翻折的性质可知∠GEF=∠BEF,从而得到∠FEB=∠BEF从而得到三角形EFG为等腰三角形;
(2)先证明△ADH≌△CB′H,从而得到DH=DB′,然后将△B′HC的周长转化为三角形B′C与DC的和即可.
解:(1)由折叠的性质可知∠GEF=∠BEF.
∵DC∥AB,
∴∠GFE=∠FEB.
∴∠FEB=∠BEF.
∴EG=FG.
∴△EFG为等腰三角形.
(2)∵四边形ABCD为矩形,
∴AD=BC.
由翻折的性质可知:BC=CB′,∠B′=∠B=90°.
∴AD=CB′,∠D=∠B′.
在△ADH和△CB′H中,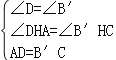 ,
,
∴△ADH≌△CB′H.
∴B′H=DH.
∴△B′HC的周长=B′C+B′H+HC=BC+DH+HC=7.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目