题目内容
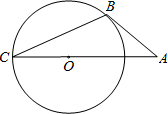
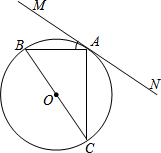
一副斜边相等的直角三角板(∠DAC=45°,∠BAC=30°),按如图所示的方式在平面内拼成一个四 边形.
边形.
(1)A,B,C,D四点在同一个圆上吗?如果在,请写出证明过程;如果不在,请说明理由;
(2)过点D作直线l∥AC,求证:l是这个圆的切线.
 边形.
边形.(1)A,B,C,D四点在同一个圆上吗?如果在,请写出证明过程;如果不在,请说明理由;
(2)过点D作直线l∥AC,求证:l是这个圆的切线.
(1)A,B,C,D四点在同一个圆上.
证明:取AC的中点O,连接OD,OB,(2分)
∵△ABC和△ADC是直角三角形,
∴OB=OD=
AC=OA=OC,(4分)
∴A,B,C,D四点在⊙O上.(5分)
(2)证明:∵Rt△ADC中,∠DAC=45°,
∴△DAC是等腰三角形,(7分)
∴OD⊥AC.(8分)
∵l∥AC,
∴OD⊥l,(9分)
∴l是⊙O的切线.(10分)

证明:取AC的中点O,连接OD,OB,(2分)
∵△ABC和△ADC是直角三角形,
∴OB=OD=
| 1 |
| 2 |
∴A,B,C,D四点在⊙O上.(5分)
(2)证明:∵Rt△ADC中,∠DAC=45°,
∴△DAC是等腰三角形,(7分)
∴OD⊥AC.(8分)
∵l∥AC,
∴OD⊥l,(9分)
∴l是⊙O的切线.(10分)


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目