ƒøƒ⁄»›
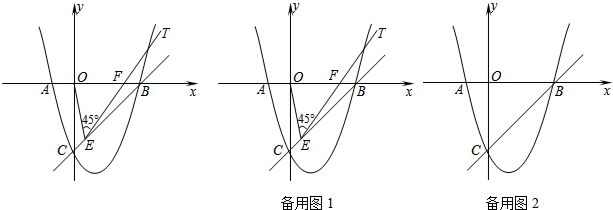
»ÁÕº£¨“—÷™≈◊ŒÔœfly=ax2-2ax+c”Îy÷·Ωª”⁄µ„C£¨”Îx÷·Ωª”⁄A°¢B¡Ωµ„£¨µ„Aµƒ◊¯±Í «£®-1£¨0£©£¨O «◊¯±Í‘≠µ„£¨«“OC=3OA£Æµ„EŒ™œfl∂ŒBC…œµƒ∂ص„£®µ„E≤ª”ε„B£¨C÷ÿ∫œ£©£¨“‘EŒ™∂•µ„◊˜°œOEF=45°„£¨…‰œflETΩªœfl∂ŒOB”⁄µ„F£Æ
£®1£©«Û≥ˆ¥À≈◊ŒÔœfl∫Ø ˝±Ì¥Ô Ω£¨≤¢÷±Ω”–¥≥ˆ÷±œflBCµƒΩ‚Œˆ Ω£ª
£®2£©«Û÷§£∫°œBEF=°œCOE£ª
£®3£©µ±°˜EOFŒ™µ»—¸»˝Ω«–Œ ±£¨«Û¥À ±µ„Eµƒ◊¯±Í£ª
£®4£©µ„PŒ™≈◊ŒÔœflµƒ∂‘≥∆÷·”Î÷±œflBCµƒΩªµ„£¨µ„M‘⁄x÷·…œ£¨µ„N‘⁄≈◊ŒÔœfl…œ£¨ «∑ҥʑ⁄“‘µ„A°¢M°¢N°¢PŒ™∂•µ„µƒ∆Ω––Àƒ±fl–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Mµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
£®1£©«Û≥ˆ¥À≈◊ŒÔœfl∫Ø ˝±Ì¥Ô Ω£¨≤¢÷±Ω”–¥≥ˆ÷±œflBCµƒΩ‚Œˆ Ω£ª
£®2£©«Û÷§£∫°œBEF=°œCOE£ª
£®3£©µ±°˜EOFŒ™µ»—¸»˝Ω«–Œ ±£¨«Û¥À ±µ„Eµƒ◊¯±Í£ª
£®4£©µ„PŒ™≈◊ŒÔœflµƒ∂‘≥∆÷·”Î÷±œflBCµƒΩªµ„£¨µ„M‘⁄x÷·…œ£¨µ„N‘⁄≈◊ŒÔœfl…œ£¨ «∑ҥʑ⁄“‘µ„A°¢M°¢N°¢PŒ™∂•µ„µƒ∆Ω––Àƒ±fl–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Mµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ

∑÷Œˆ£∫£®1£©¿˚”√“—÷™µ√≥ˆCµ„◊¯±Í£¨Ω¯∂¯¿˚”√¥˝∂®œµ ˝∑®«Û“ª¥Œ∫Ø ˝∫Õ∂˛¥Œ∫Ø ˝Ω‚Œˆ Ω£ª
£®2£©¿˚”√µ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ “‘º∞»˝Ω«–ŒµƒÕ‚Ω«÷™ ∂µ√≥ˆ°œBEF=°œCOE£ª
£®3£© ◊œ»µ√≥ˆOE£æOFº¥OE°ŸOF£¨‘Ÿ¿˚”√µ±OE=EF ±£¨µ±OF=EF ±∑÷±µ√≥ˆº¥ø…£ª
£®4£©¢ŸAPŒ™±fl£¨¥À ±Pµ„◊›◊¯±ÍŒ™2ªÚ-2£¨¢⁄APŒ™∂‘Ω«œfl£¨…ËMŒ™£®x£¨0£©‘ÚNŒ™£®-x£¨-2£©Ω¯∂¯µ√≥ˆMµ„◊¯±Í£Æ
£®2£©¿˚”√µ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ “‘º∞»˝Ω«–ŒµƒÕ‚Ω«÷™ ∂µ√≥ˆ°œBEF=°œCOE£ª
£®3£© ◊œ»µ√≥ˆOE£æOFº¥OE°ŸOF£¨‘Ÿ¿˚”√µ±OE=EF ±£¨µ±OF=EF ±∑÷±µ√≥ˆº¥ø…£ª
£®4£©¢ŸAPŒ™±fl£¨¥À ±Pµ„◊›◊¯±ÍŒ™2ªÚ-2£¨¢⁄APŒ™∂‘Ω«œfl£¨…ËMŒ™£®x£¨0£©‘ÚNŒ™£®-x£¨-2£©Ω¯∂¯µ√≥ˆMµ„◊¯±Í£Æ
Ω‚¥£∫ Ω‚£∫£®1£©°flµ„Aµƒ◊¯±Í «£®-1£¨0£©£¨‘ÚAO=1£¨OC=3OA=3£¨
Ω‚£∫£®1£©°flµ„Aµƒ◊¯±Í «£®-1£¨0£©£¨‘ÚAO=1£¨OC=3OA=3£¨
°‡CŒ™£®0£¨-3£©
°fl≈◊ŒÔœflπ˝£®-1£¨0£©∫Õ£®0£¨-3£©
°‡¥À≈◊ŒÔœfl∫Ø ˝±Ì¥Ô ΩŒ™£∫y=x2-2x-3£¨
°fly=x2-2x-3=£®x-3£©£®x+1£©£¨
°‡Bµ„◊¯±ÍŒ™£∫£®3£¨0£©£¨
…ËBC÷±œflΩ‚Œˆ ΩŒ™£∫y=kx+b£¨
£¨
Ω‚µ√£∫
£¨
÷±œflBCµƒΩ‚Œˆ Ω£∫y=x-3£ª
£®2£©°flOB=OC=3
°‡°œOCB=°œOBC=45°„
”÷°fl°œOEF+°œBEF=°œCOE+°œOCB
«“°œOEF=45°„
°‡°œBEF=°œCOE£ª
£®3£©¢Ÿ°fl°œOFE=°œBEF+°œOBC£æ45°„
°‡°œOFE£æ°œOEF
°‡OE£æOFº¥OE°ŸOF£Æ
¢⁄µ±OE=EF ±£¨
‘⁄°˜COE∫Õ°˜BEF÷–
£¨
°‡°˜COE°’°˜BEF£®AAS£©£¨
°‡BE=CO=3£Æ
π˝E◊˜ED°Õx÷·”⁄D£Æ
°‡ED=BD=BEcos45°„=
£¨
°‡OD=3-
£¨
°‡EŒ™£®3-
£¨-
£©£ª
¢€µ±OF=EF ±£¨‘Ú°œFOE=°œOEF=45°„
°‡°œOFE=90°„£Æ°‡EF°ÕOB£Æ
°‡EŒ™BCµƒ÷–µ„£¨°‡EŒ™(
£¨-
)£Æ
£®4£©∂‘≥∆÷·Œ™x=1£¨
°‡PŒ™£®1£¨-2£©£Æ
¢ŸAPŒ™±fl£¨
¥À ±Pµ„◊›◊¯±ÍŒ™2ªÚ-2£¨
¡Óx2-2x-3=2
º¥x2-2x-5=0
°‡x1=1+
£¨x2=1-
£¨
°‡NŒ™£®1+
£¨2£©ªÚ£®1-
£¨2£©£¨
π MŒ™£®3+
£¨0£©ªÚ£®3-
£¨0£©£¨
¡Óx2-2x-3=-2
º¥x2-2x-1=0£¨
°‡x1=1+
£¨x2=1-
£¨
°‡NŒ™£®1+
£¨2£©ªÚ£®1-
£¨2£©£¨
π MŒ™£®-1+
£¨0£©ªÚ£®-1-
£¨0£©£¨
¢⁄APŒ™∂‘Ω«œfl£¨
…ËMŒ™£®x£¨0£©
‘ÚNŒ™£®-x£¨-2£©
°‡x2+2x-3=-2
x2+2x-1=0
°‡x1=-1+
£¨x2=-1-
£¨
π MŒ™£®-1+
£¨0£©ªÚ£®-1-
£¨0£©£¨
◊€…œÀ˘ ˆ£∫MŒ™£®3+
£¨0£©ªÚ£®3-
£¨0£©ªÚ£®-1+
£¨0£©ªÚ£®-1-
£¨0£©£Æ
 Ω‚£∫£®1£©°flµ„Aµƒ◊¯±Í «£®-1£¨0£©£¨‘ÚAO=1£¨OC=3OA=3£¨
Ω‚£∫£®1£©°flµ„Aµƒ◊¯±Í «£®-1£¨0£©£¨‘ÚAO=1£¨OC=3OA=3£¨°‡CŒ™£®0£¨-3£©
°fl≈◊ŒÔœflπ˝£®-1£¨0£©∫Õ£®0£¨-3£©
|
°‡¥À≈◊ŒÔœfl∫Ø ˝±Ì¥Ô ΩŒ™£∫y=x2-2x-3£¨
°fly=x2-2x-3=£®x-3£©£®x+1£©£¨
°‡Bµ„◊¯±ÍŒ™£∫£®3£¨0£©£¨
…ËBC÷±œflΩ‚Œˆ ΩŒ™£∫y=kx+b£¨
|
Ω‚µ√£∫
|
÷±œflBCµƒΩ‚Œˆ Ω£∫y=x-3£ª
£®2£©°flOB=OC=3
°‡°œOCB=°œOBC=45°„
”÷°fl°œOEF+°œBEF=°œCOE+°œOCB
«“°œOEF=45°„
°‡°œBEF=°œCOE£ª
£®3£©¢Ÿ°fl°œOFE=°œBEF+°œOBC£æ45°„
°‡°œOFE£æ°œOEF
°‡OE£æOFº¥OE°ŸOF£Æ
¢⁄µ±OE=EF ±£¨
‘⁄°˜COE∫Õ°˜BEF÷–
|
°‡°˜COE°’°˜BEF£®AAS£©£¨
°‡BE=CO=3£Æ
π˝E◊˜ED°Õx÷·”⁄D£Æ
°‡ED=BD=BEcos45°„=
3
| ||
| 2 |
°‡OD=3-
3
| ||
| 2 |
°‡EŒ™£®3-
3
| ||
| 2 |
3
| ||
| 2 |
¢€µ±OF=EF ±£¨‘Ú°œFOE=°œOEF=45°„
°‡°œOFE=90°„£Æ°‡EF°ÕOB£Æ
°‡EŒ™BCµƒ÷–µ„£¨°‡EŒ™(
| 3 |
| 2 |
| 3 |
| 2 |
£®4£©∂‘≥∆÷·Œ™x=1£¨
°‡PŒ™£®1£¨-2£©£Æ
¢ŸAPŒ™±fl£¨
¥À ±Pµ„◊›◊¯±ÍŒ™2ªÚ-2£¨
¡Óx2-2x-3=2
º¥x2-2x-5=0

°‡x1=1+
| 6 |
| 6 |
°‡NŒ™£®1+
| 6 |
| 6 |
π MŒ™£®3+
| 6 |
| 6 |
¡Óx2-2x-3=-2
º¥x2-2x-1=0£¨
°‡x1=1+
| 2 |
| 2 |
°‡NŒ™£®1+
| 2 |
| 2 |
π MŒ™£®-1+
| 2 |
| 2 |
¢⁄APŒ™∂‘Ω«œfl£¨
…ËMŒ™£®x£¨0£©
‘ÚNŒ™£®-x£¨-2£©
°‡x2+2x-3=-2
x2+2x-1=0
°‡x1=-1+
| 2 |
| 2 |
π MŒ™£®-1+
| 2 |
| 2 |
◊€…œÀ˘ ˆ£∫MŒ™£®3+
| 6 |
| 6 |
| 2 |
| 2 |
µ„∆¿£∫¥ÀÂ÷˜“™øº≤È¡À¥˝∂®œµ ˝∑®«Û“ª¥Œ∫Ø ˝∫Õ∂˛¥Œ∫Ø ˝Ω‚Œˆ Ω“‘º∞∆Ω––Àƒ±fl–Œµƒ–‘÷ ∫Õµ»—¸»˝Ω«–Œµƒ–‘÷ µ»÷™ ∂£¨¿˚”√∑÷¿‡Ã÷¬€ÀºœÎµ√≥ˆ «Ω‚Âπÿº¸£Æ

¡∑œ∞≤·œµ¡–¥∞∏
œ‡πÿƒø
 C£®0£¨3£©£Æ
C£®0£¨3£©£Æ °¢C£®0£¨-3£©¡Ωµ„£¨”Îx÷·Ωª”⁄¡Ì“ªµ„B£Æ
°¢C£®0£¨-3£©¡Ωµ„£¨”Îx÷·Ωª”⁄¡Ì“ªµ„B£Æ £®2013•∫‚—Ù£©»ÁÕº£¨“—÷™≈◊ŒÔœflæ≠π˝A£®1£¨0£©£¨B£®0£¨3£©¡Ωµ„£¨∂‘≥∆÷· «x=-1£Æ
£®2013•∫‚—Ù£©»ÁÕº£¨“—÷™≈◊ŒÔœflæ≠π˝A£®1£¨0£©£¨B£®0£¨3£©¡Ωµ„£¨∂‘≥∆÷· «x=-1£Æ »ÁÕº£¨“—÷™≈◊ŒÔœfly=ax2+bx+c£®a°Ÿ0£©µƒ∂‘≥∆÷·Œ™÷±œflx=1£¨«“≈◊ŒÔœflæ≠π˝A£®-1£¨0£©°¢C£®0£¨-3£©¡Ωµ„£¨”Îx÷·Ωª”⁄¡Ì“ªµ„B£Æ
»ÁÕº£¨“—÷™≈◊ŒÔœfly=ax2+bx+c£®a°Ÿ0£©µƒ∂‘≥∆÷·Œ™÷±œflx=1£¨«“≈◊ŒÔœflæ≠π˝A£®-1£¨0£©°¢C£®0£¨-3£©¡Ωµ„£¨”Îx÷·Ωª”⁄¡Ì“ªµ„B£Æ »ÁÕº£¨“—÷™≈◊ŒÔœfly=ax2+bx+cµƒ∂•µ„ «£®-1£¨-4£©£¨«“”Îx÷·Ωª”⁄A°¢B£®1£¨0£©¡Ωµ„£¨Ωªy÷·”⁄µ„C£ª
»ÁÕº£¨“—÷™≈◊ŒÔœfly=ax2+bx+cµƒ∂•µ„ «£®-1£¨-4£©£¨«“”Îx÷·Ωª”⁄A°¢B£®1£¨0£©¡Ωµ„£¨Ωªy÷·”⁄µ„C£ª