题目内容
二次函数y=x2-4x+6的顶点坐标是顶点________，对称轴是对称轴直线________，最小值是________．
（2，2） x=2 2
分析：首先知a b c的大小，求出
和-
的大小，即可求出顶点坐标，对称轴和最小值．
解答：解；y=x2-4x+6，
这里a=1 b=-4 c=6，
∴x=-=-
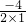=2，
y==
=2．
故答案为：二次函数y=x2-4x+6的顶点坐标是顶点 （2，2）；对称轴是对称轴直线x=2，最小值是y最小值=2．
点评：解此题的关键是对二次函数的性质的理解和掌握，知二次函数的顶点坐标，对称轴，最小值之间的关系及求法．
分析：首先知a b c的大小，求出
和-的大小，即可求出顶点坐标，对称轴和最小值．解答：解；y=x2-4x+6，
这里a=1 b=-4 c=6，
∴x=-
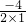=-=2，y=
==2．故答案为：二次函数y=x2-4x+6的顶点坐标是顶点 （2，2）；对称轴是对称轴直线x=2，最小值是y最小值=2．
点评：解此题的关键是对二次函数的性质的理解和掌握，知二次函数的顶点坐标，对称轴，最小值之间的关系及求法．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目