Question

【题目】下面是“作顶角为 120°的等腰三角形的外接圆”的尺规作图过程．已知：△ABC，AB＝AC，∠A＝120°．求作：△ABC 的外接圆．作法：（1）分别以点 B 和点 C 为圆心，AB 的长为半径作弧，两弧的一个交点为 O；（2）连接 BO；（3）以 O 为圆心，BO 为半径作⊙O．⊙O 即为所求作的圆．请回答：该尺规作图的依据是_______．

Answer 1

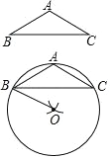
【答案】该尺规作图的依据为：四边相等的四边形是菱形、有一个角为 60°的等腰三角形是等边三角形、圆的定义．

【解析】

由作图知AB=OB=OC=AC可判定四边形ABOC为菱形，根据∠BAC=120°知∠BAO=∠CAO=60°，从而得∠BAO=∠CAO=60°，即△OAB、△OAC为等边三角形，继而由OB=OA=OC可得所求作的圆．

如图，连接OA、OC，

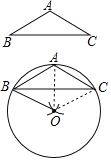
由作图知BA=BO、OC=OA，

∵AB=AC，

∴AB=OB=OC=AC，

∴四边形ABOC为菱形（四边形相等的四边形是菱形），

又∵∠BAC=120°，

∴∠BAO=∠CAO=60°，

则△OAB、△OAC为等边三角形（有一个角为60°的等腰三角形是等边三角形），

∴OB=OA=OC，

∴点A、B、C在以O为圆心、OB为半径的圆上（圆的定义），

综上，该尺规作图的依据为：四边形相等的四边形是菱形、有一个角为60°的等腰三角形是等边三角形、圆的定义．