题目内容
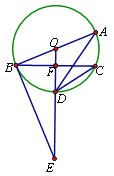
【题目】如图,点A在反比例函数y=![]() (x<0)的图象上,点B在X轴的负半轴上,AB=AO=13,线段OA的垂直平分线交线段AB于点C,△BOC的周长为23,则k的值为( )
(x<0)的图象上,点B在X轴的负半轴上,AB=AO=13,线段OA的垂直平分线交线段AB于点C,△BOC的周长为23,则k的值为( )
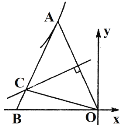
A.60B.30C.-60D.-30
【答案】C
【解析】
作AC⊥x轴于D,如图,利用垂直平分线的性质得CA=CO,再利用等腰三角形的性质和线段的等量代换可得到OB=10,接着利用等腰三角形的性质得BD=OD=5,则利用勾股定理可计算出AD=12,所以A(-5,12),然后根据反比例函数图象上点的坐标特征求k的值.
解:作AC⊥x轴于D,如图,
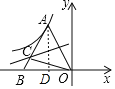
∵线段OA的垂直平分线交线段AB于点C,
∴CA=CO,
∵△BOC的周长为23,
∴OB+BC+OC=23,
∴OB+BC+CA=23,即OB+BA=23,
∴OB=23-13=10,
∵AB=AO,AD⊥OB,
∴BD=OD=5,
在Rt△AOD中,![]()
∴A(-5,12),
∴k=-5×12=-60.
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目