题目内容
已知点P的坐标为(x,y)且(x+1)2+
=0,则点P关于原点的对称点P′的坐标是( )
| 2y+3 |
A、(-1,
| ||
B、(-1,-
| ||
C、(1,-
| ||
D、(1,
|
分析:先根据非负数的性质求出x,y的值,再根据关于原点对称的两点坐标之间的关系,求出P′的坐标.
解答:解:∵(x+1)2+
=0,
∴
,
解得
,
∴点P的坐标为(-1,-
),
∴点P关于原点的对称点P′的坐标是(1,
).
故选D.
| 2y+3 |
∴
|
解得
|
∴点P的坐标为(-1,-
| 3 |
| 2 |
∴点P关于原点的对称点P′的坐标是(1,
| 3 |
| 2 |
故选D.
点评:本题主要考查了非负数的性质及平面直角坐标系中关于原点对称的两点坐标之间的关系.用到的知识点有:有限个非负数的和为零,那么每一个加数也必为零;关于原点对称的两点,横、纵坐标都是互为相反数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
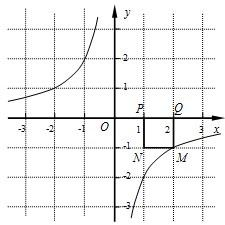 已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=- 如图,抛物线y=ax2+bx(a>0)与双曲线y=
如图,抛物线y=ax2+bx(a>0)与双曲线y= (2013•宜宾)如图,直线y=x-1与反比例函数y=
(2013•宜宾)如图,直线y=x-1与反比例函数y=