题目内容
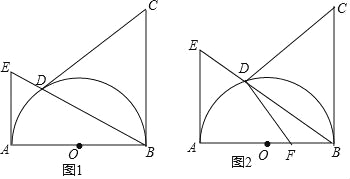
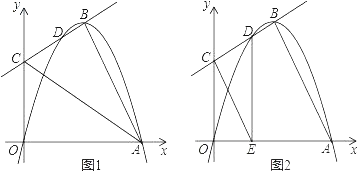
【题目】如图1,平面直角坐标系xOy中,已知抛物线y=ax2+4x与x轴交于O、A两点.直线y=kx+m经过抛物线的顶点B及另一点D(D与A不重合),交y轴于点C.
(1)当OA=4,OC=3时.
①分别求该抛物线与直线BC相应的函数表达式;
②连结AC,分别求出tan∠CAO、tan∠BAC的值,并说明∠CAO与∠BAC的大小关系;
(2)如图2,过点D作DE⊥x轴于点E,连接CE.当a为任意负数时,试探究AB与CE的位置关系?
【答案】(1)①y=﹣x2+4x,y=![]() x+3;②∠CAO>∠BAC;(2)AB∥CE,理由见解析.
x+3;②∠CAO>∠BAC;(2)AB∥CE,理由见解析.
【解析】
(1)①根据题意得出A、C的坐标,由A的坐标可求出抛物线解析式及其顶点B坐标,根据B、C坐标可得直线解析式;
②tan∠CAO=![]() ,先根据勾股定理逆定理判定△ABC是直角三角形,再根据tan∠BAC=
,先根据勾股定理逆定理判定△ABC是直角三角形,再根据tan∠BAC=![]() 可得答案;
可得答案;
(2)根据y=ax2+4x求得A(-![]() ,0)、B(-
,0)、B(-![]() ,-
,-![]() ),先求得tan∠BAO=2,再将B(-
),先求得tan∠BAO=2,再将B(-![]() ,-
,-![]() )代入y=kx+m得m=
)代入y=kx+m得m=![]() ,据此知点C(0,
,据此知点C(0,![]() ),由
),由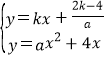 可求得E(
可求得E(![]() ,0),根据tan∠CEO=
,0),根据tan∠CEO=![]() =2知∠BAO=∠CEO,从而得出答案.
=2知∠BAO=∠CEO,从而得出答案.
(1)①∵OA=4,OC=3,
∴A(4,0),C(0,3),
将A(4,0)代入y=ax2+4x,得:16a+16=0,
解得a=﹣1,
则y=﹣x2+4x=﹣(x﹣2)2+4,
∴B(2,4),
将B(2,4),C(0,3)代入y=kx+m,得:![]() ,
,
解得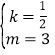 ,
,
∴y=![]() x+3;
x+3;
②tan∠CAO=![]() ,
,
∵AC2=(0﹣4)2+(3﹣0)2=25,BC2=(2﹣0)2+(4﹣3)2=5,AB2=(2﹣4)2+(4﹣0)2=20,
∴AC2=BC2+AB2,且BC=![]() ,AB=2
,AB=2![]() ,
,
∴△ABC是直角三角形,其中∠ABC=90°,
则tan∠BAC=![]() ,
,
∵tan∠CAO>tan∠BAC,
∴∠CAO>∠BAC.
(2)AB∥CE,理由如下:
由y=ax2+4x=0得x1=0,x2=﹣![]() ,则A(﹣
,则A(﹣![]() ,0),
,0),
又y=ax2+4x=a(x+![]() )2﹣
)2﹣![]() ,
,
∴顶点B的坐标为(﹣![]() ,﹣
,﹣![]() ),
),
则tan∠BAO=![]() ,
,
将B(﹣![]() ,﹣
,﹣![]() )代入y=kx+m,得:﹣
)代入y=kx+m,得:﹣![]() +m=﹣
+m=﹣![]() ,
,
解得m=![]() ,
,
∴点C(0,![]() ),即OC=
),即OC=![]() ,
,
由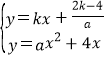 得x=﹣
得x=﹣![]() 或x=
或x=![]() ,
,
∴E(![]() ,0),
,0),
∴OE=![]() ,
,
∴tan∠CEO=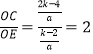 ,
,
∴tan∠BAO=tan∠CEO,
∴∠BAO=∠CEO,
∴AB∥CE.

【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?