��Ŀ����
����Ŀ�����壺�������������һ��������߶ΰ���������ηֳ�����С�����Σ�����һ���������ǵ��������Σ�����һ�������κ�ԭ�����ε������ڽǷֱ���ȣ���ô�����߶γ�Ϊԭ�����ε�����г�ָ����������磺��ͼ1������ֱ��������б���ϵ����߾���һ������г�ָ�����
![]() �ж���������������������Ǽ�����
�ж���������������������Ǽ�����![]() ����������������
����������������![]()
![]() �ȱ������αش�������г�ָ�����
�ȱ������αش�������г�ָ�����
![]() �������������һ��������һ���ǵ�����������������αش�������г�ָ�������
�������������һ��������һ���ǵ�����������������αش�������г�ָ�������
����![]() ��______���⣬����
��______���⣬����![]() ��______���⣻
��______���⣻
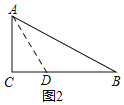
![]() ��ͼ2��
��ͼ2��![]() ��
��![]() ��
��![]() ��
��![]() ����̽��
����̽��![]() �Ƿ��������г�ָ������������ڣ��������г�ָ������ij��ȣ��������ڣ���˵�����ɣ�
�Ƿ��������г�ָ������������ڣ��������г�ָ������ij��ȣ��������ڣ���˵�����ɣ�
![]() ��ͼ3��
��ͼ3��![]() �У�
�У�![]() �����߶�CD��
�����߶�CD��![]() ������г�ָ���������
������г�ָ���������![]() �ǵ��������Σ�������з���������
�ǵ��������Σ�������з���������![]() �Ķ�����
�Ķ�����

���𰸡���1���٣��棻��2��![]() ��3��
��3��![]() ��ֵΪ
��ֵΪ![]() ��
��![]() ��
��
��������
![]() ��������г�ָ������Ķ��弴���жϣ�
��������г�ָ������Ķ��弴���жϣ�
![]() ��ͼ��
��ͼ��![]() ��ƽ���ߣ�ֻҪ֤���߶�AD������г�ָ��������ɣ����������Ǻ�����������AD�ij���
��ƽ���ߣ�ֻҪ֤���߶�AD������г�ָ��������ɣ����������Ǻ�����������AD�ij���
![]() ��2���������ۼ���
��2���������ۼ���
![]() �ȱ������β���������г�ָ�����������ȷ���Ǽ����⣻
�ȱ������β���������г�ָ�����������ȷ���Ǽ����⣻
![]() �������������һ��������һ���ǵ�����������������αش�������г�ָ���������ȷ���������⣬
�������������һ��������һ���ǵ�����������������αش�������г�ָ���������ȷ���������⣬
�ʴ�Ϊ���٣��棻
![]() ��������г�ָ������������ǣ�
��������г�ָ������������ǣ�
��ͼ��![]() ��ƽ���ߣ�
��ƽ���ߣ�
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() �ǵ��������Σ���
�ǵ��������Σ���![]() ��
��![]() ��
��
![]() �߶�AD��
�߶�AD��![]() ������г�ָ�������
������г�ָ�������
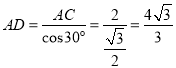 ��
��
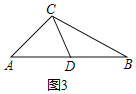
![]() ��ͼ3�У���2�����Σ�
��ͼ3�У���2�����Σ�
![]() ��
��![]() ��
��![]() ��
��![]() ʱ��
ʱ��![]()
��![]() ����
����![]()
![]() ��
��
�ɵ�![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ʱ��
ʱ��
��![]() ����
����![]()
![]() ��
��
�ɵ�![]() ��
��
��������������������![]() ��ֵΪ
��ֵΪ![]() ��
��![]() ��
��

 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�





