题目内容
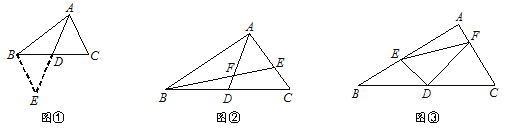
【题目】已知:Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E、F,当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证![]() .
.
![]() 当∠EDF绕
当∠EDF绕![]() 点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,![]() 、
、![]() 、
、![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.

【答案】(1)、答案见解析;(2)、![]() -
-![]() =
=![]() .
.
【解析】
试题分析:(1)、首先连接CD,得出△ECD和△FBD全等,根据△CDB的面积等于△ABC面积的一半进行说明;(2)、根据第一题同样的思路得出三角形面积之间的关系.
试题解析:(1)在图2情况下,式子成立.证明如下:
连接CD∵AB=BC,D为AB边的中点 ∴CD⊥AB,∠ACD=∠BCD=45°, ![]()
∵∠ACB=90°,D为AB边的中点 ∴CD=BD=![]() AB ∠B=45°
AB ∠B=45°
∴∠B=∠ACD ∵∠EDC+∠CDF=90°,∠CDF+∠FDB=90° ∴∠EDC=∠FDB
∴△ECD≌△FBD ∴![]()
∵![]() =
=![]() =
=![]()
又![]() ∴
∴![]()
(2)、在图3情况下,式子不成立. 猜想:![]() -
-![]() =
=![]() .
.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目