��Ŀ����
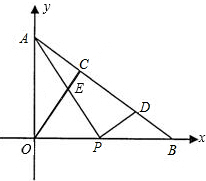 ��ƽ��ֱ�������У�Rt��OAB��������A��B�ֱ���y�ᣬx����������ϣ���O��ԭ�㣮���е�A��0��3����B��4��0����OC��Rt��OAB�ĸߣ���P��ÿ��1����λ�����ٶ����߶�OB���ɵ�O���B�˶�����˵㲻�غϣ�������P��PD��AP��AB�ڵ�D�����˶�ʱ��Ϊt�룮
��ƽ��ֱ�������У�Rt��OAB��������A��B�ֱ���y�ᣬx����������ϣ���O��ԭ�㣮���е�A��0��3����B��4��0����OC��Rt��OAB�ĸߣ���P��ÿ��1����λ�����ٶ����߶�OB���ɵ�O���B�˶�����˵㲻�غϣ�������P��PD��AP��AB�ڵ�D�����˶�ʱ��Ϊt�룮��1������AOE�����Ϊ
| 3 |
| 2 |
��2����֤����AOE�ס�PBD��
��3����PBD�ܷ��ǵ��������Σ����ܣ������ʱt��ֵ�������ܣ���˵�����ɣ�
��4����t=3ʱ��ֱ��д����ʱ
| AE |
| EP |
��������1������E��EF��OA��F����EF�ǡ�OAE�ĸߣ���֪OA�ij������ݡ�OAE������������EF��ֵ����֤�á�OEF�ס�BAO�������������������ñ����߶μ������OE�ij���Ҳ���ܵõ�E������꣮
��2������AP��PD����ô��DPB�͡�EAOͬΪ��APO����ǣ����EAO=��DPB����֤�á�AOE=��PBD���ɴ˿�֤����������������ƣ�
��3�����ڡ�APD�У���APD=90�㣬�ʡ�ADP����ǣ���BDP�Ƕ۽ǣ�����BPD�ǵ��������Σ���ô��BDP��Ϊ���ǣ���DP=BD�����ڡ�AOE�ס�PBD����ô��AOEҲ�ǵ��������Σ���OE=AE�����ݵ������������ߺ�һ������֪��AF=FO=
�����գ�1���ķ�������ͨ����OEF�ס�BAO�����EF�ij�������AEF�ס�APO�������������������ñ����߶μ������OP�ij���t��ֵ��
��4����t=3ʱ��OP=OA=3����AP=3
���ɣ�2��֤�á�AOE�ס�PBD����ôAE��PD=OA��PB������OA=3��PB=OB-OP=1�����AE=3PD������PD=x����AE=3x���á�AEC�ס�ADP�����У�
=
��������Ӱ��������Rt��ABO�����AC�ij������ù��ɶ��������EC�ı���ʽ�������Ǵ�����ʽ����ʽ�У��������x��ֵ�������ɵõ�EC��AE�ij�������AE��AP�ij������ɵõ�AE��EP��ֵ��
��2������AP��PD����ô��DPB�͡�EAOͬΪ��APO����ǣ����EAO=��DPB����֤�á�AOE=��PBD���ɴ˿�֤����������������ƣ�
��3�����ڡ�APD�У���APD=90�㣬�ʡ�ADP����ǣ���BDP�Ƕ۽ǣ�����BPD�ǵ��������Σ���ô��BDP��Ϊ���ǣ���DP=BD�����ڡ�AOE�ס�PBD����ô��AOEҲ�ǵ��������Σ���OE=AE�����ݵ������������ߺ�һ������֪��AF=FO=
| 3 |
| 2 |
��4����t=3ʱ��OP=OA=3����AP=3
| 2 |
| EC |
| PD |
| AC |
| AP |
�����1���⣺����E��EF��OA�ڵ�F��
�ߡ�AOE�����Ϊ
��OA=3��
��EF=1��
�ߡ�EOF=��ABO=90��-��BOC��
��EFO=��AOB=90�㣬
���OEF�ס�BAO��
=
����
=
������OF=
��
���E��������1��
����
��2��֤������Rt��OAB�У�OCΪб��AB���ϵĸߣ�
���EOA+��OAC=90�㣬��DBP+��OAC=90�㣬
���EOA=��DBP��
���EOA=��DBP=90��-��BOC��
 ��AEO=��PDB=90��+��PAB��
��AEO=��PDB=90��+��PAB��
���AOE�ס�PBD��
��3����PBD�����ǵ��������Σ�
�ߡ�PDB=90��+��PAB��90�㣬
�������PBD�ǵ��������Σ���PDBֻ�ܶ��ǣ���DP=DB��
����PDB�ǵ��������Σ��ߡ�AOE�ס�PBD��
���AOE�ǵ��������Σ���EA=EO��
����E��EF��AO�ڵ�F����AF=OF=
��
�ߡ�OEF�ס�BAO��
��
=
����
=
������EF=
��
�ߡ�AFE�ס�AOP��
��
=
����
=
������t=
��
�൱��PBD�ǵ���������ʱ��t=
��
��4����t=3ʱ��
=
��
�ߡ�AOE�����Ϊ
| 3 |
| 2 |
��EF=1��
�ߡ�EOF=��ABO=90��-��BOC��
��EFO=��AOB=90�㣬
���OEF�ס�BAO��
| EF |
| AO |
| OF |
| BO |
| 1 |
| 3 |
| OF |
| 4 |
| 4 |
| 3 |
���E��������1��
| 4 |
| 3 |
��2��֤������Rt��OAB�У�OCΪб��AB���ϵĸߣ�
���EOA+��OAC=90�㣬��DBP+��OAC=90�㣬
���EOA=��DBP��
���EOA=��DBP=90��-��BOC��
 ��AEO=��PDB=90��+��PAB��
��AEO=��PDB=90��+��PAB�����AOE�ס�PBD��
��3����PBD�����ǵ��������Σ�
�ߡ�PDB=90��+��PAB��90�㣬
�������PBD�ǵ��������Σ���PDBֻ�ܶ��ǣ���DP=DB��
����PDB�ǵ��������Σ��ߡ�AOE�ס�PBD��
���AOE�ǵ��������Σ���EA=EO��
����E��EF��AO�ڵ�F����AF=OF=
| 3 |
| 2 |
�ߡ�OEF�ס�BAO��
��
| EF |
| AO |
| OF |
| BO |
| EF |
| 3 |
| ||
| 4 |
| 9 |
| 8 |
�ߡ�AFE�ס�AOP��
��
| AF |
| AO |
| EF |
| PO |
| ||
| 3 |
| ||
| t |
| 9 |
| 4 |
�൱��PBD�ǵ���������ʱ��t=
| 9 |
| 4 |
��4����t=3ʱ��
| AE |
| EP |
| 3 |
| 4 |
������������Ҫ����������������ε������Լ����������ε��ж����ڽ������У���������õ������������ε����ʣ��ܹ��������߶κ���֪�߶������������δ��������ǽ�����Ĺؼ���

��ϰ��ϵ�д�
 ����5��2���ϵ�д�
����5��2���ϵ�д�
�����Ŀ
 22����ͼ��ʾ����ƽ��ֱ�������У������ߵĶ���P����ľ�����4����������x���ཻ��O��M���㣬OM=4������ABCD�ı�BC���߶ε�OM�ϣ���A��D���������ϣ�
22����ͼ��ʾ����ƽ��ֱ�������У������ߵĶ���P����ľ�����4����������x���ཻ��O��M���㣬OM=4������ABCD�ı�BC���߶ε�OM�ϣ���A��D���������ϣ�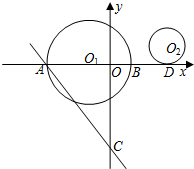 ��ƽ��ֱ�������У���O1��-4��0�����뾶Ϊ8�ġ�O1��x�ύ��A��B����A��ֱ��l��x�Ḻ�����60��ǣ��ҽ�y���ڵ�C���Ե�O2��13��5��ΪԲ�ĵ�Բ��x�����ڵ�D��
��ƽ��ֱ�������У���O1��-4��0�����뾶Ϊ8�ġ�O1��x�ύ��A��B����A��ֱ��l��x�Ḻ�����60��ǣ��ҽ�y���ڵ�C���Ե�O2��13��5��ΪԲ�ĵ�Բ��x�����ڵ�D�� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��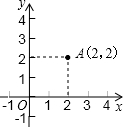 ��ͼ����ƽ��ֱ�������У���A��2��2��������x�����ҵ�P��ʹ��AOP�ǵ��������Σ���ô�������������У�������
��ͼ����ƽ��ֱ�������У���A��2��2��������x�����ҵ�P��ʹ��AOP�ǵ��������Σ���ô�������������У�������