Question

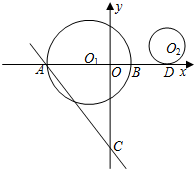在平面直角坐标中，点O₁（-4，0），半径为8的⊙O₁与x轴交于A、B，过A作直线l与x轴负方向成60°角，且交y轴于点C，以点O₂（13，5）为圆心的圆与x轴切于点D．
（1）求直线l的解析式；
（2）将⊙O₂以每秒1个单位长的速度沿x轴向左平移，当⊙O₂第一次与⊙O₁外切时，求平移的时间．

Answer 1

分析：（1）求直线的解析式，可以先求出A、C两点的坐标，就可以根据待定系数法求出函数的解析式．
（2）设⊙O₂平移t秒后到⊙O₃处与⊙O₁第一次外切于点P，⊙O₃与x轴相切于D₁点，连接O₁O₃，O₃D₁．在直角△O₁O₃D₁中，根据勾股定理，就可以求出O₁D₁，进而求出D₁D的长，得到平移的时间．

解答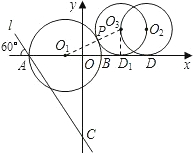：解：（1）由题意得OA=|-4|+|8|=12，
∴A点坐标为（-12，0）．
∵在Rt△AOC中，∠OAC=60°，
OC=OAtan∠OAC=12×tan60°=12

3

．
∴C点的坐标为（0，-12

3

）．
设直线l的解析式为y=kx+b，
由l过A、C两点，
得

-12 3 =b 0=-12k+b

，解得

b=-12 3 k=- 3

∴直线l的解析式为：y=-

3

x-12

3

．

（2）如图，设⊙O₂平移t秒后到⊙O₃处与⊙O₁第一次外切于点P，⊙O₃与x轴相切于D₁点，连接O₁O₃，O₃D₁．
则O₁O₃=O₁P+PO₃=8+5=13．
∵O₃D₁⊥x轴，∴O₃D₁=5，
在Rt△O₁O₃D₁中，O1D1=

O1 O 2 3 -O3 D 2 1

=

132-52

=12．
∵O₁D=O₁O+OD=4+13=17，∴D₁D=O₁D-O₁D₁=17-12=5，
∴t=

5

1

=5（秒）．
∴⊙O₂平移的时间为5秒．

点评：本题综合了待定系数法求函数解析式，以及圆的位置关系，其中两圆相切时的辅助线的作法是经常用到的．