题目内容
 如图,梯形ABCD中,AB∥CD,AB=125,AD=DC=80,问对角线BD能否把梯形分成两个相似的三角形?若不能,给出证明;若能,求出BC、BD的长.
如图,梯形ABCD中,AB∥CD,AB=125,AD=DC=80,问对角线BD能否把梯形分成两个相似的三角形?若不能,给出证明;若能,求出BC、BD的长.
解:假设能分成两个相似的三角形,
∵AB∥CD,
∴∠ABD=∠BDC.
则两个相似三角形有下面两种情况:
(1)△ABD∽△BDC
∴ =
=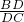 =
=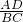 ,
,
即: =
= =
=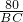 ,
,
解得:BD=100,BC=64.
(2)△ABD∽△CDB,
∴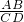 =
= =
= ,
,
即: =
= =1.
=1.
显然 ≠1,所以不能这样对应相似.
≠1,所以不能这样对应相似.
所以只能是:△ABD∽△BDC,
此时BC=64,BD=100.
分析:先假设能分成两个相似的三角形,根据两直线平行,内错角相等,可以找到一对对应顶点,写出两组相似三角形,然后利用相似三角形的性质求出BC与BD的长,对使对应边的比不等的三角形要舍去.
点评:本题考查的是相似三角形的判定与性质,根据梯形的两底平行内错角相等,找到一对对应顶点,因为另两个对应顶点不确定,所以写出两组相似三角形,再用相似三角形的性质进行计算,求出BC与BD的值.
∵AB∥CD,
∴∠ABD=∠BDC.
则两个相似三角形有下面两种情况:
(1)△ABD∽△BDC
∴
 =
=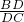 =
=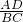 ,
,即:
 =
= =
=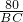 ,
,解得:BD=100,BC=64.
(2)△ABD∽△CDB,
∴
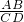 =
= =
= ,
,即:
 =
= =1.
=1.显然
 ≠1,所以不能这样对应相似.
≠1,所以不能这样对应相似.所以只能是:△ABD∽△BDC,
此时BC=64,BD=100.
分析:先假设能分成两个相似的三角形,根据两直线平行,内错角相等,可以找到一对对应顶点,写出两组相似三角形,然后利用相似三角形的性质求出BC与BD的长,对使对应边的比不等的三角形要舍去.
点评:本题考查的是相似三角形的判定与性质,根据梯形的两底平行内错角相等,找到一对对应顶点,因为另两个对应顶点不确定,所以写出两组相似三角形,再用相似三角形的性质进行计算,求出BC与BD的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
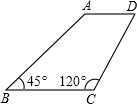 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
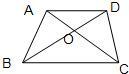 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有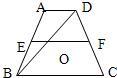 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,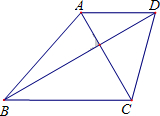 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.