��Ŀ����
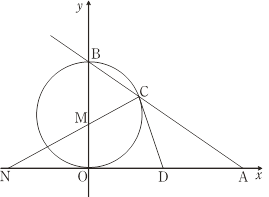
����Ŀ���ס���������֮�俪ͨ�˶���������г�����֪ÿ��2h��һ���ٶ���ͬ�Ķ������г��Ӽ׳ǿ����ҳǡ���ͼ,OA�ǵ�һ�ж������г��뿪�׳ǵ�·��s(km)������ʱ��t(h)�ĺ���ͼ��,BC��һ�д��ҳǿ����׳ǵ���ͨ�쳵��׳ǵ�·��s(km)������ʱ��t(h)�ĺ���ͼ�������ͼ�е���Ϣ������������⣺
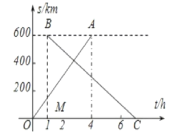
(1)��ͼ��,��ͨ�쳵����ʱ��ȵ�һ�ж������г�����ʱ��___1h(����������������)����B��������600��ʵ��������___��
(2)��ֱ����ͼ�л����ڶ��ж������г��뿪�׳ǵ�·��s(km)��ʱ��t(h)�ĺ���ͼ��
(3)����ͨ�쳵���ٶ�Ϊ100km/h��
����BC�ı���ʽ����д���Ա�����ȡֵ��Χ��
�ڵڶ��ж������г������ʱ�������ͨ�쳵����?
����ֱ��д��������ͨ�쳵����ʻ;����ӭ��������������ж������г�������ʱ����.
���𰸡���1�������ס���������֮��ľ���Ϊ600ǧ�ף���2������������3����S=100t+700���Ա����ķ�ΧΪ��1t7����2Сʱ�ۼ��Ϊ1.2Сʱ.
��������
��1������ͼ��ó���ͨ�쳵����ʱ��ȵ�һ�ж������г�����ʱ����1Сʱ���ҵ�B���������ʾ�ס���������֮��ľ���Ϊ600ǧ�ף�
��2������ÿ��2h��һ���ٶ���ͬ�Ķ������г��Ӽ׳ǿ����ҳǻ���ͼ�ɣ�
��3������ֱ��BC�Ľ���ʽS=kt+b������B��C�������ɣ�
����ֱ��MN�Ľ���ʽ���������ʽ��������ֱ���ཻ�г����̽�ɣ�
�۸���������ͨ�쳵��ӭ��������������ж������г�����ʽ�г����̽�ɣ�
(1)��ͼ��ɵã���ͨ�쳵����ʱ��ȵ�һ�ж������г�����ʱ����1Сʱ��
��B���������ʾ�ס���������֮��ľ���Ϊ600ǧ�ף�
�ʴ�Ϊ�������ס���������֮��ľ���Ϊ600ǧ�ף�
(2)��ͼ��ʾ��
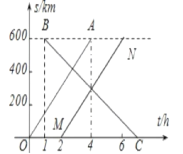
(3)����Ϊ�ס���������֮��ľ���Ϊ600ǧ�ף���ͨ�쳵���ٶ�Ϊ100km/h��
����ͨ�쳵��ʱ��Ϊ600��100=6,�ɵõ�C������Ϊ(7,0)��
��ֱ��BC�Ľ���ʽS=kt+b��
��B(1,600),C(7,0)��
��![]() ��
��
��ã�![]() ��
��
����ֱ��BC�Ľ���ʽΪ��S=100t+700��
�Ա����ķ�ΧΪ��1t7��
����ֱ��MN�Ľ���ʽΪ��S=k1t+b1��
��M(2,0),N(6,600)��
�� ��
��
��ã�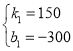 ��
��
��S=150t300��
��ֱ��BC�Ľ���ʽΪ��S=100t+700��
��ɵã�150t300=100t+700��
��ã�t=4��
42=2.
�𣺵ڶ��ж������г�����2Сʱ������ͨ�쳵������
�۸������⣬��һ�ж������г�����ʽΪ��y=150t��
��������ͨ�쳵����ʻ;����ӭ��������������ж������г�������ʱ����Ϊ��
150t=100t+700��
��ã�t=2.8.
��42.8=1.2
��������ͨ�쳵����ʻ;����ӭ��������������ж������г�������ʱ����Ϊ1.2Сʱ.

 Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�����Ŀ��ijУΪ�˽��ߡ����꼶ѧ����������ˮ����ȫ֪ʶ��������������ߡ����꼶�������ȡ50��ѧ�����в��ԣ����Գɼ����ٷ��ƣ����������������ͷ�����������Ϣ���£�
a�����꼶�ɼ�Ƶ���ֲ�ֱ��ͼ��

b�����꼶�ɼ���![]() ��һ����ǣ�70 72 74 75 76 76 77 77 77 78 79
��һ����ǣ�70 72 74 75 76 76 77 77 77 78 79
c���ߡ����꼶�ɼ���ƽ��������λ�����£�
�꼶 | ƽ���� | ��λ�� |
�� | 76.9 | m |
�� | 79.2 | 79.5 |
����������Ϣ���ش��������⣺
��1������β����У����꼶��80�����ϣ���80�֣������� ���ˣ�
��2������m��ֵΪ�� ����
��3������β����У����꼶ѧ��������꼶ѧ���ҵijɼ�����78�֣����ж���λѧ���ڸ����꼶������˭����ǰ����˵�����ɣ�
��4����У���꼶ѧ����400�ˣ�����ȫ���μӴ˴β��ԣ���������꼶�ɼ�����ƽ����76.9�ֵ�������