题目内容
(1)如图1,AB为⊙O的直径,直线l交⊙O于C、D,过A、B分别作l的垂线,垂足分别为E、F,经推证,可得出结论EC=DF,证明过程中辅助线的添法是(2)上题中,若把l继续向上平行移动,使弦CD与直径AB交于P(P与A、B不重合),在其它条件不变的情况下,请你在图2中将变化后的图形画出来,标好对应字母,并写出与(1)相应成立的结论等式,并判断你写的结论是否成立,若不成立,请说明理由;若成立,请给予证明,结论
(3)若(2)中⊙O半径为5cm,∠CPB=150°,且AP:BP=7:3,试求弦CD的长度.

分析:(1)作辅助线,过O作OG⊥EF于G,由垂径定理可得:CG=DG,又AE∥OG∥BF,OA=OB,
由平行线等分线段定理得:EG=FG.故:EG-CG=FG-DG,即:EC=DF;
(2)证明过程同(1),可得:EC=DF;
(3)作辅助线,连接OD,由∠CPA=150°,可得:∠OPG=30°,AB=10,AP:BP=7:3,可得AP=7,BP=3,OP=2.
OG=sin30°×OP=1.
在Rt△OGD中,运用勾股定理可将DG求出,由垂径定理可得:CD=2DG.
由平行线等分线段定理得:EG=FG.故:EG-CG=FG-DG,即:EC=DF;
(2)证明过程同(1),可得:EC=DF;
(3)作辅助线,连接OD,由∠CPA=150°,可得:∠OPG=30°,AB=10,AP:BP=7:3,可得AP=7,BP=3,OP=2.
OG=sin30°×OP=1.
在Rt△OGD中,运用勾股定理可将DG求出,由垂径定理可得:CD=2DG.
解答:解:
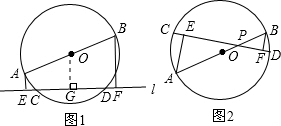
(1)过O作OG⊥EF于G,可得:CG=DG
∵AE⊥CD,OG⊥CD,BF⊥CD,∴AE∥OG∥BF
∵OA=OB,∴EG=FG
∴EG-CG=FG-DG
∴EC=DF
(2)EC=DF依然成立,证明过程同(1)
过O作OG⊥EF于G,可得:CG=DG
∵AE⊥CD,OG⊥CD,BF⊥CD,∴AE∥OG∥BF
∵OA=OB,∴EG=FG
∴EG-CG=FG-DG
∴EC=DF
(3)连接OD
∵⊙O的半径为5,AP:BP=7:3,∴AP=7,BP=3,OP=2
∵∠CPB=150°,∴∠OPG=30°
在Rt△OPG中,OG=sin30°×OP=1
在Rt△OGD中,DG=
=
=2
故:CD=2DG=4
.

(1)过O作OG⊥EF于G,可得:CG=DG
∵AE⊥CD,OG⊥CD,BF⊥CD,∴AE∥OG∥BF
∵OA=OB,∴EG=FG
∴EG-CG=FG-DG
∴EC=DF
(2)EC=DF依然成立,证明过程同(1)
过O作OG⊥EF于G,可得:CG=DG
∵AE⊥CD,OG⊥CD,BF⊥CD,∴AE∥OG∥BF
∵OA=OB,∴EG=FG
∴EG-CG=FG-DG
∴EC=DF
(3)连接OD
∵⊙O的半径为5,AP:BP=7:3,∴AP=7,BP=3,OP=2
∵∠CPB=150°,∴∠OPG=30°
在Rt△OPG中,OG=sin30°×OP=1
在Rt△OGD中,DG=
| OD2-OG2 |
| 52-12 |
| 6 |
故:CD=2DG=4
| 6 |
点评:本题主要考查垂径定理的应用,在解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
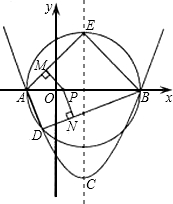 已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A,B两点,A(-1,0).
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A,B两点,A(-1,0).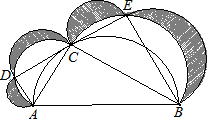 如图,以AB为直径作半圆与直角梯形ABED另一腰DE相切于C点,再分别以AC、BC、
如图,以AB为直径作半圆与直角梯形ABED另一腰DE相切于C点,再分别以AC、BC、 (2012•永安市质检)如图,以AB为直径的⊙O经过点C,D是AB延长线上一点,且DC=AC,∠CAB=30°.
(2012•永安市质检)如图,以AB为直径的⊙O经过点C,D是AB延长线上一点,且DC=AC,∠CAB=30°. 如图,以AB为直径的⊙O与直线CD相切于点E,且AC⊥CD,BD⊥CD,AC=8cm,BD=2cm,求四边形ACDB的面积.
如图,以AB为直径的⊙O与直线CD相切于点E,且AC⊥CD,BD⊥CD,AC=8cm,BD=2cm,求四边形ACDB的面积.