Question

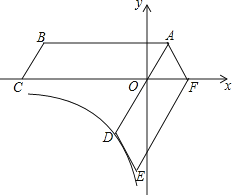
【题目】小强为了测量一幢高楼高AB，在旗杆CD与楼之间选定一点P．测得旗杆顶C视线PC与地面夹角∠DPC＝36°，测楼顶A视线PA与地面夹角∠APB＝54°，量得P到楼底距离PB与旗杆高度相等，等于10米，量得旗杆与楼之间距离为DB＝36米，小强计算出了楼高，楼高AB是多少米？

Answer 1

【答案】楼高AB是26米．

【解析】

试题分析: 因为∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,

所以∠DCP=∠APB=54°,根据,,判定△CPD≌△PAB,根据全等三角形的性质进而得出AB的长.

试题解析:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,

∴∠DCP=∠APB=54°,

在△CPD和△PAB中,

∵,

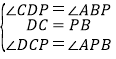∴△CPD≌△PAB（ASA）,

∴DP=AB,

∵DB=36,PB=10,

∴AB=36﹣10=26（m）,

答:楼高AB是26米．