题目内容
【题目】在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数 ![]() 的图象上,第二象限内的点B在反比例函数
的图象上,第二象限内的点B在反比例函数 ![]() 的图象上,连接OA、OB,若OA⊥OB,OB=
的图象上,连接OA、OB,若OA⊥OB,OB= ![]() OA,则k= .
OA,则k= .
【答案】﹣ ![]()
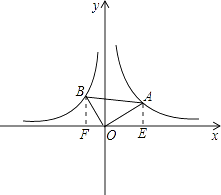
【解析】解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
设点A的坐标为(a, ![]() ),点B的坐标为(b,
),点B的坐标为(b, ![]() ),
),
∵∠AOE+∠BOF=90°,∠OBF+∠BOF=90°,
∴∠AOE=∠OBF,
又∵∠BFO=∠OEA=90°,
∴△OBF∽△AOE,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
则 ![]() =﹣
=﹣ ![]() b①,a=
b①,a= ![]() ②,
②,
① ②可得:﹣2k=1,
解得:k=﹣ ![]() .
.
所以答案是:﹣ ![]() .
.
【考点精析】关于本题考查的反比例函数的图象,需要了解反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能得出正确答案.

练习册系列答案
相关题目



