题目内容
【题目】有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C= ![]() ,其中正确的有( )
,其中正确的有( ) 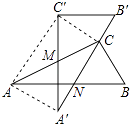
A.2个
B.3个
C.4个
D.5个
【答案】C
【解析】解:①∵点M是线段AC、线段A′C′的中点,AC=2, ∴AM=MC=A′M=MC′=1,
∵∠MA′C=30°,
∴∠MCA′=∠MA′C=30°,
∴∠A′MC=180°﹣30°﹣30°=120°,
∴∠A′MA=180°﹣A′MC=180°﹣120°=60°,
∴∠AMA′=∠C′MC=60°,
∴△AA′M是等边三角形,
∴AA′=AM=1,故①正确;
②∵∠A′CM=30°,∠MCC′=60°,
∴∠ACA′=∠A′CM+∠MCC′=90°,
∴CC′⊥A′C,故②正确;
③∵∠A′CA=∠NAC=30°,∠BCN=∠CBN=60°,
∴AN=NC=NB,故③正确;
④∵△AA′M≌△C′CM,
∴AA′=CC′,∠MAA′=∠C′CM=60°,
∴AA′∥CC′,
∴四边形AA′CC′是平行四边形,
∵∠AA′C=∠AA′M+∠MA′C=90°,
四边形AA′CC′为矩形,故④正确;
⑤AN= ![]() AB=
AB= ![]() ,
,
∠NAA′=30°,∠AA′N=90°,
∴A′N= ![]() AN=
AN= ![]() ,故⑤错误;
,故⑤错误;
故选:C.
①根据旋转的性质,可得AM=MC=A′M=MC′=1,根据等腰三角形的性质,可得∠MCA′,根据等边三角形的判定,可得答案;
②根据垂线的性质:过直线外一点与已知直线垂直的直线只有一条,可得答案;
③根据等腰三角形的判定,可得答案
④根据平行四边形的判定,可得四边形AA′CC′是平行四边形,再根据有一个角是直角的平行四边形是矩形,可得答案;
⑤根据勾股定理可得BA的长,根据AB与AN的关系,可得AN的长,根据直角三角形的性质,可得答案.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案