题目内容
【题目】如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,AD平分∠MAC,交BC于点D,AM交BE于点G.
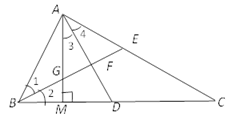
求证:(1) ∠BAM=∠C;
(2)判断直线BE与线段AD之间的关系,并说明理由.
【答案】(1)证明见解析;
(2) BE垂直平分AD ,理由见解析.
【解析】分析:(1)根据余角的性质即可得到结论;(2)由AD平分∠MAC,得到∠3=∠4,根据三角形的外角的性质得到∠BAD=∠ADB,推出△BAD是等腰三角形,于是得到结论.
本题解析:

(1)∵AM⊥BC
∴∠ABC+∠BAM =90°
∵∠BAC=90°
∠ABC+∠C =90°
∴∠BAM=∠C
(2)BE垂直平分AD
理由:
∵AD平分∠MAC
∴∠3=∠4
∵∠BAD=∠BAM+∠3
∠ADB=∠C+∠4
∠BAM=∠C
∴∠BAD=∠ADB
∴△BAD是等腰三角形
又∵∠3=∠4
∴BE垂直平分AD

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目