Question

【题目】在平面坐标系中，对于点和点，给出如下定义：

若，则称点为点的变限点。例如：点的变限点的坐标，点 的变限点的坐标。

（1）点的变限点的坐标是 ；点的变限点的坐标是 .

（2）已知直线与轴交于点，点在直线上，其变限点为，若（为坐标原点）的面积等于，求点的坐标.

（3）已知点在函数的图象上，其变限点的纵坐标的取值范围是，求的取值范围.

Answer 1

【答案】(1) , (2) (3)

【解析】

(1)直接根据变限点的定义，则称点为点的变限点，代入点直接得出答案.

(2) 由直线与轴交于点求得A点坐标为，并代入（为坐标原点）的面积等于，可知点Q的纵坐标有-3和3两种，分别代入求解即可.

(3)由点Q在函数图像上联立求出b’的取值，并由变限点的纵坐标的取值范围是，进行代入最小值b’分别求出x即可.

解：（1）根据变限点的定义，将点代入可得其变限点的坐标是点Q，将点代入可得有其变限点的坐标是

（2）由直线与轴交于点求得A点坐标为，点Q在函数的图像上，有显然有当b’=-3时，-3=-x+2，有x=5，当b’=3时，-3=x-2，有x=-1，所以Q点坐标为

（3）点Q必在函数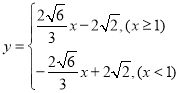的图像上，则有即当x=1时，b’取得最小值当时，求得当若则由图像可知