��Ŀ����
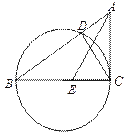
����Ŀ����ͼ��1������֪��ABC�У���BAC=90�㣬AB=AC��AE�ǹ�A��һ��ֱ�ߣ���B��C��A��E����࣬BD��AE��D��CE��AE��E 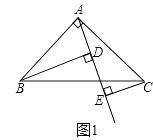
��1����˵����BD=DE+CE��
��2����ֱ��AE��A����ת��ͼ��2��λ��ʱ��BD��CE���������������䣬��BD��DE��CE�Ĺ�ϵ��Σ���ֱ��д������� 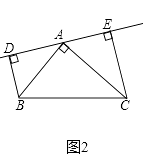
��3����ֱ��AE��A����ת��ͼ��3��λ��ʱ��BD��CE���������������䣬��BD��DE��CE�Ĺ�ϵ��Σ���ֱ��д�����������˵�����ɣ� 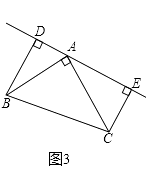
���𰸡�
��1��֤�����ߡ�BAC=90�㣬
���BAD+��EAC=90�㣬
�֡�BD��AE��CE��AE��
���BDA=��AEC=90�㣬
��BAD+��ABD=90�㣬
���ABD=��EAC��
�֡�AB=AC��
���ABD�ա�CAE��
��BD=AE��AD=CE��
��AE=AD+DE=CE+DE��
��BD=DE+CE
��2���⣺ͬ���ɵã�DE=BD+CE
��3���⣺ͬ���ɵã�DE=BD+CE
����������1��֤����ABD�ա�CAE������֤��BD=AE��AD=CE����AE=AD+DE=CE+DE������֤�ã���2����3��ͼ�α任�ˣ����ǣ�1���е�ȫ�ȹ�ϵ��û�иı䣬���BD��DE��CE�Ĺ�ϵ��û�иı䣮
�����㾫����������Ҫ������ȫ�������ε����ʺ���ת�����ʵ����֪ʶ�㣬��Ҫ����ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ�����ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��˲�����ȷ�����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�