题目内容
【题目】如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.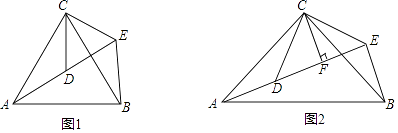
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°.
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=90°,CF为△DCE中DE边上的高,试猜想AE,CF,BE之间的关系,并证明你的结论.
【答案】
(1)
①证明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,
∴∠ACB=∠DCE=180°﹣2×50°=80°,
∵∠ACB=∠ACD_∠DCB,∠DCE=∠DCB+∠BCE,
∴∠ACD=∠BCE,
∵△ACB,△DCE都是等腰三角形,
∴AC=BC,DC=EC,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE.
②解:∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∵点A、D、E在同一直线上,且∠CDE=50°,
∴∠ADC=180°﹣∠CDE=130°,
∴∠BEC=130°,
∵∠BEC=∠CED+∠AEB,∠CED=50°,
∴∠AEB=∠BEC﹣∠CED=80°
(2)
解:结论:AE=2CF+BE.
理由:∵△ACB,△DCE都是等腰直角三角形,
∴∠CDE=∠CED=45°,
∵CF⊥DE,
∴∠CFD=90°,DF=EF=CF,
∵AD=BE,
∴AE=AD+DE=BE+2CF.
【解析】(1)①欲证明AD=BE,只要证明△ACD≌△BCE即可.②由△ACD≌△BCE,推出∠ADC=∠BEC,由点A、D、E在同一直线上,且∠CDE=50°,推出∠ADC=180°﹣∠CDE=130°,推出∠BEC=130°,根据∠AEB=∠BEC﹣∠CED计算即可.(2)由(1)可知AD=BE,只要证明DE=2CF即可解决问题.

练习册系列答案
相关题目



