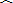Question

如图，正方形ABCD内接于⊙O，⊙O的半径为2，以圆心O为顶点作∠MON，使∠MON=90°，OM、ON分别与⊙O交于点E、F，与正方形ABCD的边交于点G、H，则由OE、OF、

EF

及正方形ABCD的边围成的图形（阴影部分）的面积S=______．

Answer 1

过点O作OP⊥AB，OQ⊥BC，则OP=OQ，
在△OPH和△OQG中，

∠HOP=∠GOQ ∠OPH=∠OQG OQ=OP

，
故可得△OPH≌△OQG，从而可得四边形OHBG与正方形OQBP的面积，
∵圆的半径为2，
∴OQ=OP=

2

，
S_阴影=S_扇形OEF-S_OHBG=S_扇形OEF-S_OQBP=

90π×22

360

-

2

×

2

=π-2．
故答案为：π-2．