��Ŀ����
����Ŀ���������¶��壺��һ���ı����д����������ߵ�ƽ���͵���һ���Խ��ߵ�ƽ������Ƹ��ı���Ϊ�����ı��Σ�
��1�������ı����У��ǹ����ı��ε�Ϊ ������д��ż��ɣ�
�پ��Σ�����һ����Ϊֱ�ǵ������ı��Σ�����һ����Ϊ60�������Σ�
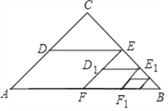
��2����ͼ������ABC�ƶ���B��˳ʱ�뷽����ת60���õ���DBE����DCB=30��������AD��DC��CE��
����֤����BCE�ǵȱ������Σ�
����֤���ı���ABCD�ǹ����ı��Σ�
���𰸡���1���٢�����2����֤������������֤��������
�������������������1���ɹ����ı��εĶ���������ı��ε����ʣ���ɵó���
��2��������ת�����ʿ�֪��ABC�ա�DBE���Ӷ��ɵ�BC=BE���ɡ�CBE=60���ɵ���BCEΪ�ȱ������Σ����ɢٿɵá�BCE=60�����Ӷ���֪��DCE��ֱ�������Σ������ù��ɶ������ɽ�����⣮
���������
��1������ͼ��
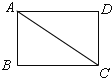
���ı���ABCD�Ǿ��Σ�
���B=90����
��AB2+BC2=AC2��
���������ǹ����ı��Σ�
����ͼ��
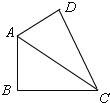
�ߡ�B=90����
��AB2+BC2=AC2��
������һ����Ϊֱ�ǵ��ı����ǹ����ı��Σ�
����һ����Ϊ60�������Σ��ڱ߱���û��ֱ�ǣ����Բ����㹴���ı��εĶ��壬
�ʴ�Ϊ�٢���
��2���١ߡ�ABC�Ƶ�B˳ʱ����ת��60������DBE��
��BC=BE����CBE=60����
������BCE��
BC=BE����CBE=60��
���BCE�ǵȱ������Σ�
�ڡߡ�BCE�ǵȱ������Σ�
��BC=CE����BCE=60����
�ߡ�DCB=30����
���DCE=��DCB+��BCE=90����
��Rt��DCE����DC2+CE2=DE2��
��DE=AC��BC=CE��
��DC2+BC2=AC2��
���ı���ABCD�ǹ����ı��Σ�