题目内容
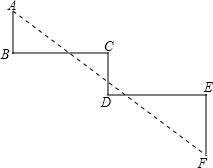 如图,已知∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=DE=8,EF=6,则A、F两点间的距离是
如图,已知∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=DE=8,EF=6,则A、F两点间的距离是
- A.16

- B.20
- C.20

- D.24
B
分析:过F作FG⊥AB,交AB的延长线于G,分别求出Rt△AGF两直角边的长,再根据勾股定理解答即可.
解答: 解:过F作FG⊥AB,交AB的延长线于G,
解:过F作FG⊥AB,交AB的延长线于G,
在Rt△AGF中,AG=AB+BG=AB+CD+EF=12,GF=BC+DE=16,
∴AF= =
= =20.
=20.
故选B.
点评:主要是作辅助线,构造直角三角形,再利用勾股定理计算.
分析:过F作FG⊥AB,交AB的延长线于G,分别求出Rt△AGF两直角边的长,再根据勾股定理解答即可.
解答:
 解:过F作FG⊥AB,交AB的延长线于G,
解:过F作FG⊥AB,交AB的延长线于G,在Rt△AGF中,AG=AB+BG=AB+CD+EF=12,GF=BC+DE=16,
∴AF=
 =
= =20.
=20.故选B.
点评:主要是作辅助线,构造直角三角形,再利用勾股定理计算.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
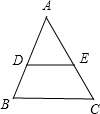 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
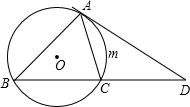 =2,∠ADC=30°
=2,∠ADC=30°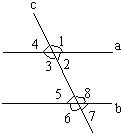 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=