题目内容
平面直角坐标系中,⊙O的圆心在坐标原点,半径为2,点A的坐标为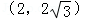 ,直线AB为⊙O的切线,B为切点.则B点的坐标为 .
,直线AB为⊙O的切线,B为切点.则B点的坐标为 .
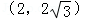 ,直线AB为⊙O的切线,B为切点.则B点的坐标为 .
,直线AB为⊙O的切线,B为切点.则B点的坐标为 .(2,0),(﹣1, )
)
 )
)过点A作圆的两条切线,AB,AC,切点分别为点B,C,连接OC,作CD⊥AB于点D
∴AB⊥OB,CD⊥AB,OC⊥AC
∵圆半径为2,点A的坐标为(2,2 ),
),
∴B点坐标为(2,0)
又∵∠ACD+∠DCO=90°,∠ACD+∠A=90°,
∴∠DCO=∠A,∠ADC=∠CEO
∴△OEC≌△CDA
∴
假设CE=x,OE=y,
∵AD=AB﹣BD=2 ﹣y,CD=2+x,co=2,AC=2
﹣y,CD=2+x,co=2,AC=2

解以上方程可以求出:x=1,y=
所以C点的坐标为(﹣1, )
)

∴AB⊥OB,CD⊥AB,OC⊥AC
∵圆半径为2,点A的坐标为(2,2
 ),
),∴B点坐标为(2,0)
又∵∠ACD+∠DCO=90°,∠ACD+∠A=90°,
∴∠DCO=∠A,∠ADC=∠CEO
∴△OEC≌△CDA
∴

假设CE=x,OE=y,
∵AD=AB﹣BD=2
 ﹣y,CD=2+x,co=2,AC=2
﹣y,CD=2+x,co=2,AC=2

解以上方程可以求出:x=1,y=

所以C点的坐标为(﹣1,
 )
)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
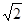 ,-
,-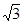 ),先将点A向右平移3个单位长度,然后向上平移3
),先将点A向右平移3个单位长度,然后向上平移3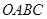 的顶点
的顶点 的坐标是(3,4),则顶点
的坐标是(3,4),则顶点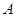 、
、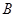 的坐标分别是_________________..
的坐标分别是_________________..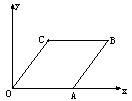
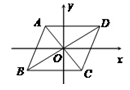
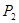 (a+6, b+2),请画出上述平移后的
(a+6, b+2),请画出上述平移后的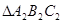 ,并写出点
,并写出点 、
、 的坐标;
的坐标;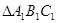 的位置关系(直接写出结果).
的位置关系(直接写出结果).
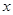 轴上确定一点P,使△AOP为等腰三角形,符合条件的点P共有_________个。
轴上确定一点P,使△AOP为等腰三角形,符合条件的点P共有_________个。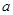 ,-l),与点B(4,
,-l),与点B(4,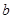 )关于
)关于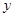 轴对称,则
轴对称,则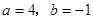
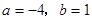
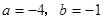
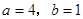
 -3,2
-3,2 轴上,则
轴上,则