题目内容
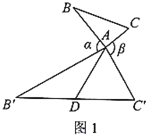
【题目】定义:如图1,在![]() 中,把
中,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() )并延长一倍得到
)并延长一倍得到![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 并延长一倍得到
并延长一倍得到![]() ,连接
,连接![]() .当
.当![]() 时,称
时,称![]() 是
是![]() 的“倍旋三角形”,
的“倍旋三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“倍旋中线”.
的“倍旋中线”.
特例感知:
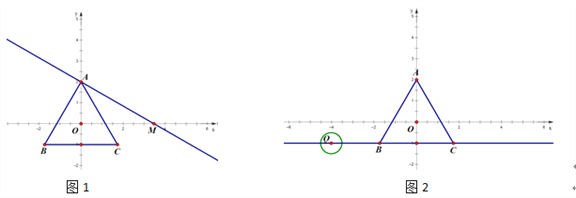
(1)如图1,当![]() ,
,![]() 时,则“倍旋中线”
时,则“倍旋中线”![]() 长为______;如图2,当
长为______;如图2,当![]() 为等边三角形时,“倍旋中线”
为等边三角形时,“倍旋中线”![]() 与
与![]() 的数量关系为______;
的数量关系为______;
猜想论证:
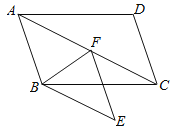
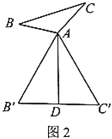
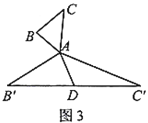
(2)在图3中,当![]() 为任意三角形时,猜想“倍旋中线”
为任意三角形时,猜想“倍旋中线”![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
【答案】(1)①4,②![]() ;(2)
;(2)![]() ,证明见解析.
,证明见解析.
【解析】
(1)如图1,首先证明![]() ,再根据直角三角形斜边上的中线等于斜边的一半即可解决问题;如图2,过点A作
,再根据直角三角形斜边上的中线等于斜边的一半即可解决问题;如图2,过点A作![]() ,易证
,易证![]() ,根据
,根据![]() 易得结论.
易得结论.
(2)延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]() 易证四边形
易证四边形![]() 是平行四边形,再证明
是平行四边形,再证明![]() 得
得![]() ,故可得结论.
,故可得结论.
(1)如图1,

∵![]() ,
,![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]()
∵BC=4,
∴![]() ,
,
∵D是![]() 的中点,
的中点,
∴AD=![]()
![]() ;
;
如图2,

∵![]() ,
,![]() ,
,
∴![]()
根据“倍旋中线”知![]() 等腰三角形,
等腰三角形,
过A作![]() ,垂足为
,垂足为![]()
∴![]() ,
,![]() ,
,![]()
∵D是等边三角形![]() 的边
的边![]() 的中点,
的中点,
![]() 且
且![]()
∴![]()
∴![]()
∴![]()
(2)结论:![]()
理由:如图,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]()
∵![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()


练习册系列答案
相关题目