题目内容
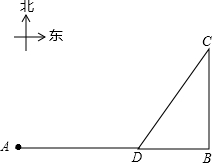 小岛A在码头B的正西方向,A、B相距40海里.上午9点,一渔船和一游艇同时出发,渔船以20海里/时的速度从B码头向正北出海作业,游艇以25海里/时的速度从A岛返回B码头.一段时间后,渔船因故障停航在C处并发出讯号.游艇在D处收到讯号后直接向渔船驶去,上午11点到达C处.游艇在上午几点收到讯号?
小岛A在码头B的正西方向,A、B相距40海里.上午9点,一渔船和一游艇同时出发,渔船以20海里/时的速度从B码头向正北出海作业,游艇以25海里/时的速度从A岛返回B码头.一段时间后,渔船因故障停航在C处并发出讯号.游艇在D处收到讯号后直接向渔船驶去,上午11点到达C处.游艇在上午几点收到讯号?
分析:设出发x小时后渔船发出讯号,根据小岛A在码头B的正西方向,A、B相距40海里.上午9点,一渔船和一游艇同时出发,渔船以20海里/时的速度从B码头向正北出海作业,游艇以25海里/时的速度从A岛返回B码头.一段时间后,渔船因故障停航在C处并发出讯号.游艇在D处收到讯号后直接向渔船驶去,上午11点到达C处,可列方程求解.
解答:解:设出发x小时后渔船发出讯号,
由题意得:(40-25x)2+(20x)2=[25(11-9-x)]2(5分)
解这个方程,得x1=1,x2=-
(不合题意,舍去)(7分)
∴9+1=10(点).(8分)
答;游艇在上午10点收到讯号.(9分)
由题意得:(40-25x)2+(20x)2=[25(11-9-x)]2(5分)
解这个方程,得x1=1,x2=-
| 9 |
| 4 |
∴9+1=10(点).(8分)
答;游艇在上午10点收到讯号.(9分)
点评:本题考查理解题意的能力,B,C,D所在的位置是直角三角形,根据勾股定理可列方程求出解.

练习册系列答案
相关题目
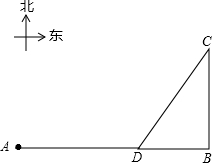 小岛A在码头B的正西方向,A、B相距40海里.上午9点,一渔船和一游艇同时出发,渔船以20海里/时的速度从B码头向正北出海作业,游艇以25海里/时的速度从A岛返回B码头.一段时间后,渔船因故障停航在C处并发出讯号.游艇在D处收到讯号后直接向渔船驶去,上午11点到达C处.游艇在上午几点收到讯号?
小岛A在码头B的正西方向,A、B相距40海里.上午9点,一渔船和一游艇同时出发,渔船以20海里/时的速度从B码头向正北出海作业,游艇以25海里/时的速度从A岛返回B码头.一段时间后,渔船因故障停航在C处并发出讯号.游艇在D处收到讯号后直接向渔船驶去,上午11点到达C处.游艇在上午几点收到讯号?
