题目内容
【题目】如图,等腰三角形ABC的底边BC的长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.

【答案】8
【解析】
连接AD交EF与点M′,连结AM,由线段垂直平分线的性质可知AM=MB,则BM+DM=AM+DM,故此当A、M、D在一条直线上时,MB+DM有最小值,然后依据要三角形三线合一的性质可证明AD为△ABC底边上的高线,依据三角形的面积为12可求得AD的长.
解:连接AD交EF与点M′,连结AM.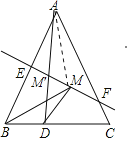
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=![]() BCAD=
BCAD=![]() ×4×AD=12,解得AD=6,
×4×AD=12,解得AD=6,
∵EF是线段AB的垂直平分线,
∴AM=BM.
∴BM+MD=MD+AM.
∴当点M位于点M′处时,MB+MD有最小值,最小值6.
∴△BDM的周长的最小值为DB+AD=2+6=8.
故答案为8.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目