题目内容
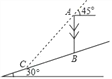
【题目】已知,平面直角坐标系中,A在x轴正半轴,B(0,1),∠OAB=30°.

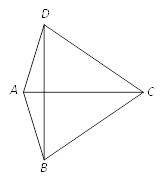
(1)如图1,已知AB=2.点C在y轴的正半轴上,当△ABC为等腰三角形时,直接写出点C的坐标为 ;
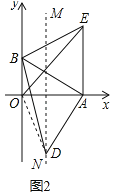
(2)如图2,以AB为边作等边△ABE,AD⊥AB交OA的垂直平分线于D,求证:BD=OE;
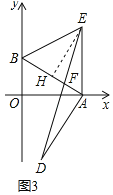
(3)如图3,在(2)的条件下,连接DE交AB于F,求![]() 的值.
的值.
【答案】(1)(0,3);(2)见解析;(3)![]()
【解析】
(1)由条件得出BC=AB=2, OC=OB+BC=3,从而可得到点C的坐标为(0,3);
(2)连接OD,证明△OAD是等边三角形,得出AO=AD,再证明△ABD≌△AEO(SAS),即可得出结论;
(3)作EH⊥AB于H,通过HL证明Rt△AEH≌Rt△BAO,得到EH=AO=AD,再通过AAS证明△HFE≌△AFD,得出EF=DF,即可求出![]() 的值.
的值.
(1)解:∵B(0,1),
∴OB=1,
∵AB=2,点C在y轴的正半轴上,△ABC为等腰三角形,
∴BC=AB=2,
∴OC=OB+BC=3,
∴点C的坐标为(0,3),
故答案为:(0,3);
(2)证明:连接OD,如图2所示:
∵△ABE是等边三角形,
∴AB=AE,∠BAE=60°,
∵∠OAB=30°,
∴∠OAE=30°+60°=90°,
∵AD⊥AB,
∴∠DAB=90°=∠OAE,∠OAD=90°﹣30°=60°,
∵MN是OA的垂直平分线,
∴OD=AD,
∴△OAD是等边三角形,
∴AO=AD,
在△ABD和△AEO中,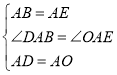 ,
,
∴△ABD≌△AEO(SAS),
∴BD=OE;
(3)解:作EH⊥AB于H,如图3所示:
∵△ABE是等边三角形,EH⊥AB,
∴AH=![]() AB,
AB,
∵∠AOB=90°,∠OAB=30°,
∴OB=![]() AB,
AB,
∴AH=OB,
在Rt△AEH和Rt△BAO中,![]() ,
,
∴△AEH≌△BAO(HL),
∴EH=AO=AD,
在△HFE和△AFD中,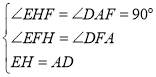 ,
,
∴△HFE≌△AFD(AAS),
∴EF=DF,
∴DE=2DF,
∴![]() =
=![]() .
.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案