题目内容
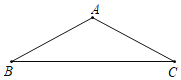
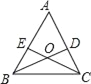
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )
A. 5对 B. 6对 C. 7对 D. 8对
【答案】C
【解析】
题中相等的角有:∠ABC=∠ACB、∠ADB=∠AEC=90°、∠BOE=∠COD、∠EAC=∠DAB,根据这些相等角可得出的相似三角形有:
△ADB∽△AEC(∠A=∠A,∠ADB=∠AEC);
△BEC∽△CDB(∠BEC=∠CDB,∠ABC=∠ACB);
△BOE∽△COD(∠BEC=∠CDB,∠BOE=∠COD);
△COD∽△CAE(∠ACE=∠OCD,∠CDO=∠CEA);
同理可证得:△BOE∽△BAD、△BOE∽△CAE、△COD∽△BAD;
∵在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高;
∴∠ABC=∠ACB,∠BEC=∠CDB=90°
∴△BEC∽△CDB
∵∠EOB=∠DOC,∠BEC=∠CDB=90°
∴△BEO∽△CDO
∵∠ABD=∠ABD,∠BEO=∠BDA=90°
∴△BEO∽△BDA
同理△CDO∽△CEA;
∵∠A=∠A,∠AEC=∠ADB=90°
∴△AEC∽△ADB
∴共有7对相似三角形.
故选C.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目