��Ŀ����
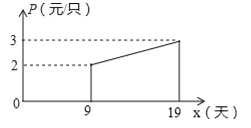
����Ŀ��������ij��ҵ������Ӧ���������·�չ���ĺ��٣��з���һ���²�Ʒ����֪�з����������ֲ�Ʒ�ijɱ�Ϊ30Ԫ/��������������y������������ۼ�x��Ԫ/�����ĺ�������ʽΪ��![]() ��
��
��1������ҵ���۸ò�Ʒ��õ�������ΪW����Ԫ������ֱ��д��������W����Ԫ�������ۼ�x��Ԫ/�����ĺ�������ʽ��
��2�����ò�Ʒ���ۼ�x��Ԫ/����Ϊ����ʱ����ҵ���۸ò�Ʒ��õ��������������������Ƕ��٣�
��3������ҵ���۸ò�Ʒ������������750��Ԫ����ȷ���ò�Ʒ���ۼ�x��Ԫ/������ȡֵ��Χ��
���𰸡���1��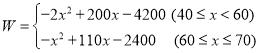 ����2���ò�Ʒ���ۼ�xΪ50Ԫ/��ʱ����ҵ���۸ò�Ʒ��õ���������������������800��Ԫ����3��45��x��55��
����2���ò�Ʒ���ۼ�xΪ50Ԫ/��ʱ����ҵ���۸ò�Ʒ��õ���������������������800��Ԫ����3��45��x��55��
��������
�����������1�����ݣ�������=���ۼ۩��ɱ������������������x��ȡֵ��Χ���к�����ϵʽ��
��2������1�����������κ����䷽�����ݶ��κ��������ʿɵ�����ֵ������ȽϺ�ɵô𰸣�
��3����������֪W��750�����й���x�IJ���ʽ�����ɵ�x�ķ�Χ��
�����������1����40��x��60ʱ��W=��x��30������2x+140��=![]() ����60��x��70ʱ��W=��x��30������x+80��=
����60��x��70ʱ��W=��x��30������x+80��=![]() ��
��
����������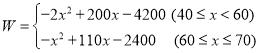 ��
��
��2����40��x��60ʱ��W=![]() =
=![]() ���൱x=50ʱ��Wȡ�����ֵ�����ֵΪ800��Ԫ��
���൱x=50ʱ��Wȡ�����ֵ�����ֵΪ800��Ԫ��
��60��x��70ʱ��W=![]() =
=![]() ���൱x��55ʱ��W��x���������С���൱x=60ʱ��Wȡ�����ֵ�����ֵΪ��
���൱x��55ʱ��W��x���������С���൱x=60ʱ��Wȡ�����ֵ�����ֵΪ��![]() =600����800��600���൱x=50ʱ��Wȡ�����ֵ800���𣺸ò�Ʒ���ۼ�xΪ50Ԫ/��ʱ����ҵ���۸ò�Ʒ��õ���������������������800��Ԫ��
=600����800��600���൱x=50ʱ��Wȡ�����ֵ800���𣺸ò�Ʒ���ۼ�xΪ50Ԫ/��ʱ����ҵ���۸ò�Ʒ��õ���������������������800��Ԫ��
��3����40��x��60ʱ����W��750�ã�![]() ��750����ã�45��x��55����60��x��70ʱ��W�����ֵΪ600��750����Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ���ۼ�x��Ԫ/������ȡֵ��ΧΪ45��x��55��
��750����ã�45��x��55����60��x��70ʱ��W�����ֵΪ600��750����Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ���ۼ�x��Ԫ/������ȡֵ��ΧΪ45��x��55��