题目内容
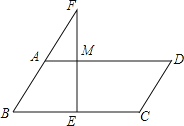
【题目】已知,在△ABC中,E,M,N分别是AB,AC,BC的中点,CF∥AB,连接MN,连接并延长EM,与直线CF交于F,连接FN交直线AB于点D,交AC于O点.
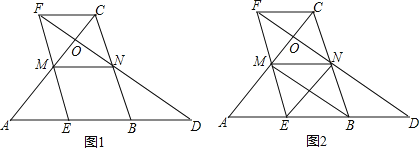
(1)如图(1),BA=BC,求证:四边形FMNC为菱形;
(2)如图(2),连接MB,NE,在不添加任何辅助线的情况下,请直接写出图(2)中的所有平行四边形(BE为边的除外).
【答案】(1)见解析;(2)所有平行四边形(BE为边的除外)有:FMNC,MAEN,MBDN,FMBN,MENC.
【解析】
试题分析:(1)首先利用三角形中位线的性质得出ME![]()
![]() BC,MN
BC,MN![]()
![]() AB,进而利用平行四边形的判定和菱形的判定方法得出即可;
AB,进而利用平行四边形的判定和菱形的判定方法得出即可;
(2)利用三角形中位线的性质结合平行四边形的判定得出即可.
(1)证明:∵E,M,N分别是AB,AC,BC的中点,BA=BC,
∴ME![]()
![]() BC,MN
BC,MN![]()
![]() AB,
AB,
∴四边形MEBN是平行四边形,
又∵ME=MN,
∴四边形FMNC为菱形;
(2)解:所有平行四边形(BE为边的除外)有:FMNC,MAEN,MBDN,FMBN,MENC.

练习册系列答案
相关题目