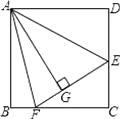
题目内容
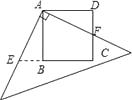
【题目】已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:CB2=ABDB;
(2)若⊙O的半径为2,∠BCP=30°,求图中阴影部分的面积.
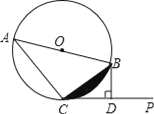
【答案】(1)证明见解析;
(2)阴影部分的面积=![]()
【解析】试题分析:(1)由CP是 ⊙O的切线,得出∠BCD=∠BAC,AB是直径,得出∠ACB=90°,所以∠ACB=∠CDB=90°,得出结论△ACB∽△CDB,从而得出结论;
(2)求出△OCB是正三角形,阴影部分的面积=S扇形OCB-S△OCB=![]() .
.
试题解析:
(1)提示:先证∠ACB=∠CDB=90°,
再证∠BAC=∠BCD,
得△ACB∽△CDB,
∴![]()
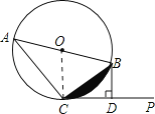
(2)解:如图,连接OC,
∵直线CP是⊙O的切线,∠BCP=30°,
∴∠COB=2∠BCP=60°,
∴△OCB是正三角形,
∵⊙O的半径为2,
∴S△OCB=![]() ,S扇形OCB=
,S扇形OCB= ![]() ,
,
∴阴影部分的面积=S扇形OCB-S△OCB=![]() .
.

练习册系列答案
相关题目
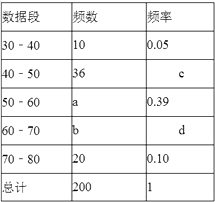
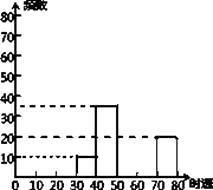
【题目】用甲、乙两种原料配制某种饮料,这两种原料的维生素C含量及购买两种原料的价格如表:
原料 | 甲 | 乙 |
维生素C的含量/(单位/kg) | 600 | 100 |
原料价格/(元/kg) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,且购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量应满足的范围.