题目内容
【题目】如图1,有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形,如图2,其中,三个正方形围成的三角形是直角三角形.再经过一次“生长”后,变成图3;“生长”10次后,如果继续“生长”下去,它将变得更加“枝繁叶茂”.
随着不断地“生长”,形成的图形中所有正方形的面积和也随之变化.若生长n次后,变成的图中所有正方形的面积用Sn表示,求回答:
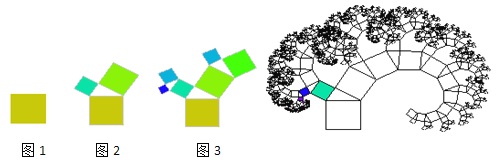
(1)S0= ,S1= ,S2= ,S3= ;
(2)S0+S1+S2+…+S10= .
【答案】(1)1,2,3,4;(2)66.
【解析】试题分析:(1)求出每一次生长后所生长出的四边形面积,找出变化规律即可;
(2)根据(1)中的规律即可得出结论.
解:(1)如图所示,
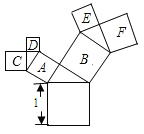
∵正方形的面积为1,
∴第一次生长后长出的三角形面积为SA+SB=1;
第二次生长后长出的三角形面积为SC+SD+SE+SF=1;
第三次生长后长出的三角形面积为:1;
第四次生长后长出的三角形面积为:1;
∴S0=1,S1=2,S2=3,S3=4.
故答案为:1,2,3,4;
(2)根据(1)中的规律可知,S0+S1+S2+…+S10=1+2+3+4+5+6+7+8+9+10+11=66.
故答案为:66.

练习册系列答案
相关题目