ƒøƒ⁄»ð
°æƒø°ø”––Ì∂ý¥˙ ˝∫„µ» Ωø…“‘”√Õº–Œµƒ√ʪ˝¿¥±Ì 棨»ÁÕº![]() £¨À¸±Ì æ¡À
£¨À¸±Ì æ¡À![]()
![]() Õº
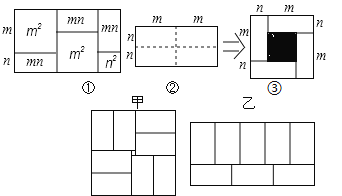
Õº![]() «Ω´“ª∏ˆ≥§2m°¢øÌ2nµƒ≥§∑Ω–Œ£¨—ÿÕº÷––Èœþ∆Ω∑ΩŒ™ÀƒøÈ–°≥§∑Ω–Œ£¨»ª∫Û‘Ÿ∆¥≥…“ª∏ˆ’˝∑Ω–Œ
«Ω´“ª∏ˆ≥§2m°¢øÌ2nµƒ≥§∑Ω–Œ£¨—ÿÕº÷––Èœþ∆Ω∑ΩŒ™ÀƒøÈ–°≥§∑Ω–Œ£¨»ª∫Û‘Ÿ∆¥≥…“ª∏ˆ’˝∑Ω–Œ![]() Õº
Õº![]() £¨‘ÚÕº
£¨‘ÚÕº![]() ÷–µƒ“ı”∞≤ø∑÷µƒ’˝∑Ω–Œµƒ±þ≥§µ»”⁄______
÷–µƒ“ı”∞≤ø∑÷µƒ’˝∑Ω–Œµƒ±þ≥§µ»”⁄______![]() ”√∫¨m°¢nµƒ¥˙ ˝ Ω±Ì æ
”√∫¨m°¢nµƒ¥˙ ˝ Ω±Ì æ![]()
![]() «Î”√¡Ω÷÷≤ªÕ¨µƒ∑Ω∑®¡–¥˙ ˝ Ω±Ì æÕº
«Î”√¡Ω÷÷≤ªÕ¨µƒ∑Ω∑®¡–¥˙ ˝ Ω±Ì æÕº![]() ÷–“ı”∞≤ø∑÷µƒ√ʪ˝£Æ
÷–“ı”∞≤ø∑÷µƒ√ʪ˝£Æ
∑Ω∑®![]() ______∑Ω∑®
______∑Ω∑®![]() ______
______
![]() «Îƒ„π€≤ÏÕº–Œ
«Îƒ„π€≤ÏÕº–Œ![]() £¨–¥≥ˆ»˝∏ˆ¥˙ ˝ Ω
£¨–¥≥ˆ»˝∏ˆ¥˙ ˝ Ω![]() °¢
°¢![]() °¢mnπÿœµµƒµ» Ω£∫______£ª
°¢mnπÿœµµƒµ» Ω£∫______£ª
![]() ∏˘æð
∏˘æð![]() Â÷–µƒµ»¡øπÿœµ£¨Ω‚戻Áœ¬Œ £∫»Ù“—÷™
Â÷–µƒµ»¡øπÿœµ£¨Ω‚戻Áœ¬Œ £∫»Ù“—÷™![]() £¨
£¨![]() £¨‘Ú
£¨‘Ú![]() ______£ª
______£ª
![]() –°√˜”√8∏ˆ“ª—˘¥Ûµƒ≥§∑Ω–Œ
–°√˜”√8∏ˆ“ª—˘¥Ûµƒ≥§∑Ω–Œ![]() ≥§acm£¨øÌ
≥§acm£¨øÌ![]() ∆¥Õº£¨∆¥≥ˆ¡À»ÁÕºº◊°¢““µƒ¡Ω÷÷Õº∞∏£¨Õº∞∏º◊ «“ª∏ˆ’˝∑Ω–Œ£¨Õº∞∏““ «“ª∏ˆ¥Ûµƒ≥§∑Ω–Œ£¨Õº∞∏º◊µƒ÷–º‰¡Ùœ¬¡À±þ≥§ «2cmµƒ’˝∑Ω–Œ–°∂¥
∆¥Õº£¨∆¥≥ˆ¡À»ÁÕºº◊°¢““µƒ¡Ω÷÷Õº∞∏£¨Õº∞∏º◊ «“ª∏ˆ’˝∑Ω–Œ£¨Õº∞∏““ «“ª∏ˆ¥Ûµƒ≥§∑Ω–Œ£¨Õº∞∏º◊µƒ÷–º‰¡Ùœ¬¡À±þ≥§ «2cmµƒ’˝∑Ω–Œ–°∂¥![]() ‘Ú
‘Ú![]() µƒ÷µŒ™______£Æ
µƒ÷µŒ™______£Æ
°æ¥∞∏°ø£®1£©m-n£ª£®2£©![]() £ª
£ª![]() £ª£®3£©
£ª£®3£©![]() £ª£®4£©9£ª£®5£©4.
£ª£®4£©9£ª£®5£©4.
°æΩ‚Œˆ°ø
![]() “ı”∞≤ø∑÷µƒ’˝∑Ω–Œµƒ±þ≥§Œ™
“ı”∞≤ø∑÷µƒ’˝∑Ω–Œµƒ±þ≥§Œ™![]() £ª
£ª
![]() ∑Ω∑®
∑Ω∑®![]() £∫“ı”∞≤ø∑÷µƒ√ʪ˝
£∫“ı”∞≤ø∑÷µƒ√ʪ˝![]() ¥Û’˝∑Ω–Œµƒ√ʪ˝
¥Û’˝∑Ω–Œµƒ√ʪ˝![]() ∏ˆ–°≥§∑Ω–Œµƒ√ʪ˝£ª∑Ω∑®
∏ˆ–°≥§∑Ω–Œµƒ√ʪ˝£ª∑Ω∑®![]() £∫±Ì æ≥ˆ–°’˝∑Ω–Œµƒ±þ≥§Œ™
£∫±Ì æ≥ˆ–°’˝∑Ω–Œµƒ±þ≥§Œ™![]() £¨º¥ø…Ω‚¥£ª
£¨º¥ø…Ω‚¥£ª
![]() ¥Û’˝∑Ω–Œµƒ√ʪ˝ºı»•4∏ˆ–°≥§∑Ω–Œµƒ√ʪ˝º¥ø…µ√≥ˆ“ı”∞≤ø∑÷µƒ√ʪ˝£¨“≤ø…µ√≥ˆ»˝∏ˆ¥˙ ˝ Ω
¥Û’˝∑Ω–Œµƒ√ʪ˝ºı»•4∏ˆ–°≥§∑Ω–Œµƒ√ʪ˝º¥ø…µ√≥ˆ“ı”∞≤ø∑÷µƒ√ʪ˝£¨“≤ø…µ√≥ˆ»˝∏ˆ¥˙ ˝ Ω![]() °¢
°¢![]() °¢mn÷ƺ‰µƒµ»¡øπÿœµ£ª
°¢mn÷ƺ‰µƒµ»¡øπÿœµ£ª
![]() ∏˘æð
∏˘æð![]() À˘µ√≥ˆµƒπÿœµ Ω£¨ø…«Û≥ˆ
À˘µ√≥ˆµƒπÿœµ Ω£¨ø…«Û≥ˆ![]() µƒ÷µ£ª
µƒ÷µ£ª
![]() ¿˚”√Õº–Œ√ʪ˝÷ƺ‰πÿœµµ√≥ˆ
¿˚”√Õº–Œ√ʪ˝÷ƺ‰πÿœµµ√≥ˆ![]() º¥ø…«Û≥ˆ£Æ
º¥ø…«Û≥ˆ£Æ
![]() “ı”∞≤ø∑÷µƒ’˝∑Ω–Œµƒ±þ≥§Œ™
“ı”∞≤ø∑÷µƒ’˝∑Ω–Œµƒ±þ≥§Œ™![]() £ª
£ª
π ¥∞∏Œ™£∫![]() £Æ
£Æ
![]() ∑Ω∑®
∑Ω∑®![]() £∫“ı”∞≤ø∑÷µƒ√ʪ˝
£∫“ı”∞≤ø∑÷µƒ√ʪ˝![]() ¥Û’˝∑Ω–Œµƒ√ʪ˝
¥Û’˝∑Ω–Œµƒ√ʪ˝![]() ∏ˆ–°≥§∑Ω–Œµƒ√ʪ˝£¨
∏ˆ–°≥§∑Ω–Œµƒ√ʪ˝£¨
À˘“‘“ı”∞≤ø∑÷µƒ√ʪ˝Œ™£∫![]() £ª
£ª
∑Ω∑®![]() £∫±Ì æ≥ˆ–°’˝∑Ω–Œµƒ±þ≥§Œ™
£∫±Ì æ≥ˆ–°’˝∑Ω–Œµƒ±þ≥§Œ™![]() £¨
£¨
À˘“‘“ı”∞≤ø∑÷µƒ√ʪ˝![]() £Æ
£Æ
π ¥∞∏Œ™£∫![]() £ª
£ª![]() £Æ
£Æ
![]() £ª
£ª
π ¥∞∏Œ™£∫![]() £Æ
£Æ
![]() £ª
£ª
π ¥∞∏Œ™£∫9£Æ
![]() £¨
£¨
![]() µƒ÷µŒ™4£Æ
µƒ÷µŒ™4£Æ
π ¥∞∏Œ™£∫4£Æ

 ÷±Õ®πÛ÷ð√˚–£÷Ð≤‚‘¬øº÷±Õ®√˚–£œµ¡–¥∞∏
÷±Õ®πÛ÷ð√˚–£÷Ð≤‚‘¬øº÷±Õ®√˚–£œµ¡–¥∞∏



