题目内容
【题目】先阅读下面的内容，再解决问题，例题：若m2+2mn+2n2﹣6n+9=0，求m和n的值． 解：∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴（m+n）2+（n﹣3）2=0
∴m+n=0，n﹣3=0
∴m=﹣3，n=3
问题
（1）若△ABC的三边长a、b、c都是正整数，且满足a2+b2﹣6a﹣6b+18+|3﹣c|=0，请问△ABC是什么形状？说明理由．
（2）若x2+4y2﹣2xy+12y+12=0，求xy的值．
（3）已知a﹣b=4，ab+c2﹣6c+13=0，则a+b+c= ．
【答案】
（1）解：△ABC是等边三角形．理由如下：
由题意得（a﹣3）2+（b﹣3）2+|3﹣c|=0，
∴a=b=c=3，
∴△ABC是等边三角形．
（2）解：由题意得（x﹣y）2+3（y+2）2=0…4′
∴x=y=﹣2．
∴xy= 
（3）3
【解析】（3）∵a﹣b=4，即a=b+4，代入得：（b+4）b+c2﹣6c+13=0， 整理得：（b2+4b+4）+（c2﹣6c+9）=（b+2）2+（c﹣3）2=0，
∴b+2=0，且c﹣3=0，即b=﹣2，c=3，a=2，
则a+b+c=2﹣2+3=3．
所以答案是：3．
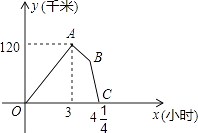
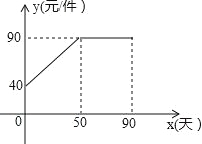
应用题作业本系列答案
【题目】 （2016湖北随州第23题）九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天） | 1 | 30 | 60 | 90 |
每天销售量p（件） | 198 | 140 | 80 | 20 |
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
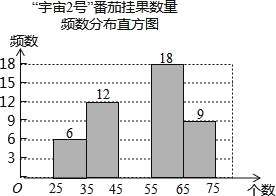
【题目】 2016海南省第21题）在太空种子种植体验实践活动中，为了解“宇番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x（单位：个），并绘制如下不完整的统计图表：
“宇番2号”番茄挂果数量统计表
挂果数量x（个） | 频数（株） | 频率 |
25≤x＜35 | 6 | 0.1 |
35≤x＜45 | 12 | 0.2 |
45≤x＜55 | a | 0.25 |
55≤x＜65 | 18 | b |
65≤x＜75 | 9 | 0.15 |
请结合图表中的信息解答下列问题：
（1）统计表中，a= ，b= ；
（2）将频数分布直方图补充完整；
（3）若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x＜45”所对应扇形的圆心角度数为 °；
（4）若所种植的“宇番2号”番茄有1000株，则可以估计挂果数量在“55≤x＜65”范围的番茄有 株．
