Question

【题目】在平面直角坐标系xOy中，四边形OABC是矩形，点B的坐标为（4，3），反比例函数y= 的图象经过点B．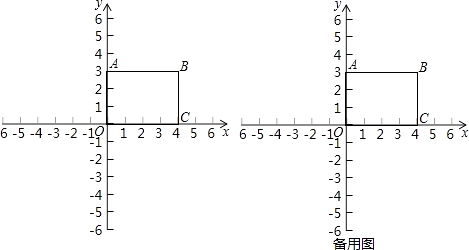

（1）求反比例函数的解析式；
（2）一次函数y=ax﹣1的图象与y轴交于点D，与反比例函数y= 的图象交于点E，且△ADE的面积等于6，求一次函数的解析式；
（3）在（2）的条件下，直线OE与双曲线y= （x＞0）交于第一象限的点P，将直线OE向右平移 个单位后，与双曲线y= （x＞0）交于点Q，与x轴交于点H，若QH= OP，求k的值．

Answer 1

【答案】
（1）解：∵反比例函数y= 的图象经过点B（4，3），

∴ =3，

∴m=12，

∴反比例函数解析式为y=

（2）解：∵四边形OABC是矩形，点B（4，3），

∴A（0，3），C（4，0），

∵一次函数y=ax﹣1的图象与y轴交于点D，

∴点D（0，﹣1），AD=4，设点E（xE，yE），

∵△ADE的面积=6，

∴ AD|xE|=6，

∴xE=±3，

∵点E在反比例函数y= 图象上，

∴E（3，4），或（﹣3，﹣4），

当E（3，4）在一次函数y=ax﹣1上时，

4=3a﹣1，

∴a= ，

∴一次函数解析式为y= x﹣1，

当点（﹣3，﹣4）在一次函数y=ax﹣1上时，

﹣4=﹣3a﹣1，

∴a=1，

∴一次函数解析式为y=x﹣1，

综上所述一次函数解析式为y=x﹣1或y= x﹣1

（3）解：由（2）可知，直线OE解析式为y= x，设点P（xP，yP），取OP中点M，则OM= OP，

∴M（ xP， xP），

∴Q（ xP+ ， xP），

∴H（ ，0），

∵点P、Q在反比例函数y= 图象上，

∴xP xP=（ xP+ ） xP，

∴xP= ，

∴P（ ， ），

∴k= ．

【解析】（1）利用待定系数法即可解决．（2）设点E（xE ， yE），由△ADE的面积=6，得 AD|xE|=6，列出方程即可解决．（3）设点P（xP ， yP），取OP中点M，则OM= OP，则M（ xP ， xP），Q（ xP+ ， xP），列出方程求出xP即可解决问题．
【考点精析】本题主要考查了矩形的性质和坐标与图形变化-平移的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等；新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点；连接各组对应点的线段平行且相等才能正确解答此题．