题目内容
如图，⊙O的直径AB=12，CD是⊙O的弦，CD⊥AB，垂足为P，且BP : AP="1" : 5.则CD的长为 （ ）
A． | B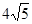． | C． | D． |
B.
试题分析：连接OC，由垂径定理可知点P为CD的中点。由AB=12，且BP : AP="1" : 5可求BP的长，从而OP长可求，在Rt△OPC中，根据勾股定理，即可得出PC，即可得出CD．
连接OC，如图：
∵弦CD⊥AB，AB=12，BP:AP=1:5
∴BP=2
∴OP=6-2=4
在Rt△OEC中，
∴CD=2CP=
故选B.
考点: 1.垂径定理；2.勾股定理.
练习册系列答案
相关题目
、
、
、
是圆上的点，
则
度．
米，∠CAD＝30°，请你帮助文物学家完成下面两项工作：
，AC=4，点O是AC的中点；回答下列问题：
，