题目内容
如图,梯形ABCD中,BC∥AD,∠ABC=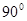 ,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
(1)求PQ经过O 点时的运动时间t;
(2)求s与t的函数关系式,并求s的最大值;
(3)如图(2),若AB的中点为H,DK=1,过H作HT∥AD,交BD于T,交BK于G,求G在正方形PQMN内部时t的取值范围。

【答案】
解:(1)t=5.
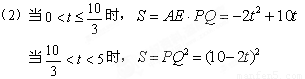
当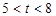 时,
时,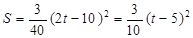
(3)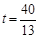 或
或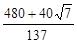 或
或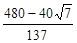
【解析】(1)根据△BOC∽△DOA,利用相似三角形对应高的比等于相似比,得到△BOC的BC边的高.从而得出点E的运动时间;
(2)分类讨论当点E在不同位置时,重叠部分的面积.

练习册系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.