题目内容
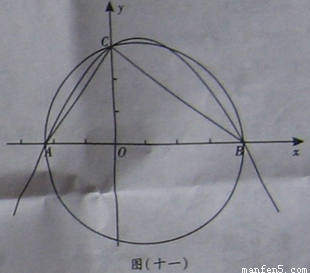
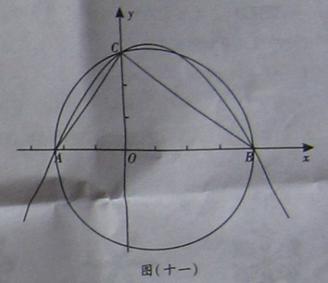
如图(十一)所示,在平面直角坐标系Oxy中,已知点A(-,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C.(1)求∠ACB的度数;
(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形.若存在,则求出所有
 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.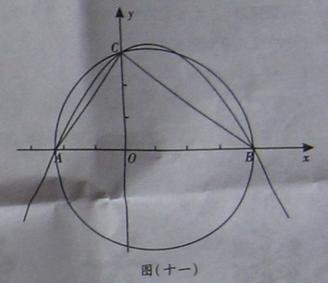
(1) ∵以AB为直径的圆恰好经过点C ∴∠ACB=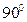
(2) ∵△AOC∽△ABC ∴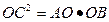 ∵A(-,0),点C(0,3),∴
∵A(-,0),点C(0,3),∴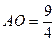
 ∴
∴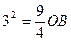 ∴
∴ 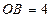 ∴B(4,0) 把 A、B、C三点坐标代入得
∴B(4,0) 把 A、B、C三点坐标代入得 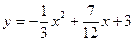
(3)
1)OD="OB" , D在OB 的中垂线上,过D作DH⊥OB,垂足是H 则H 是OB 中点。DH=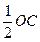
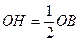 ∴D
∴D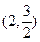
2) BD="BO " 过D作DG⊥OB,垂足是G ∴OG:OB="CD:CB " DG:OC=1:5
∴ OG:4="1:5 " DG:3="1:5 " ∴OG=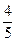 DG=
DG=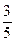 ∴D(
∴D(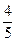 ,
,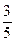 )解析:
)解析:
本题考察了相似、勾股定理、抛物线的解析式求解等知识,运用平行于三角形一边的直线截其他两边所得的三角形与原三角形相似构建比例式,求解点到坐标轴的距离,进而得出相应的坐标。难度中等
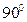
(2) ∵△AOC∽△ABC ∴
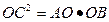 ∵A(-,0),点C(0,3),∴
∵A(-,0),点C(0,3),∴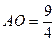
 ∴
∴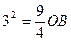 ∴
∴ 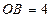 ∴B(4,0) 把 A、B、C三点坐标代入得
∴B(4,0) 把 A、B、C三点坐标代入得 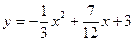
(3)
1)OD="OB" , D在OB 的中垂线上,过D作DH⊥OB,垂足是H 则H 是OB 中点。DH=
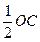
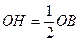 ∴D
∴D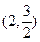
2) BD="BO " 过D作DG⊥OB,垂足是G ∴OG:OB="CD:CB " DG:OC=1:5
∴ OG:4="1:5 " DG:3="1:5 " ∴OG=
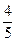 DG=
DG=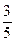 ∴D(
∴D(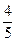 ,
,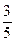 )解析:
)解析:本题考察了相似、勾股定理、抛物线的解析式求解等知识,运用平行于三角形一边的直线截其他两边所得的三角形与原三角形相似构建比例式,求解点到坐标轴的距离,进而得出相应的坐标。难度中等

练习册系列答案
相关题目
 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.
 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.
 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.
 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.