题目内容
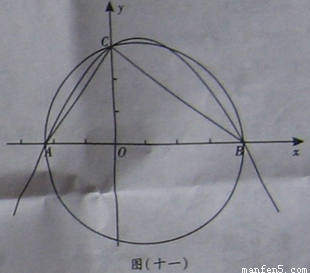
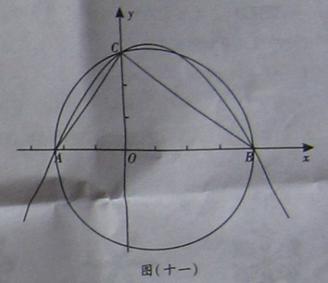
如图(十一)所示,在平面直角坐标系Oxy中,已知点A(-,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C.
(1)求∠ACB的度数;
(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形.若存在,则求出所有 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.
【答案】
(1) ∵以AB为直径的圆恰好经过点C ∴∠ACB=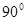
(2) ∵△AOC∽△ABC ∴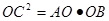 ∵A(-,0),点C(0,3),∴
∵A(-,0),点C(0,3),∴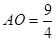
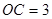 ∴
∴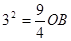 ∴
∴ 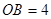 ∴B(4,0) 把 A、B、C三点坐标代入得
∴B(4,0) 把 A、B、C三点坐标代入得
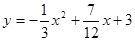
(3)
1)OD=OB , D在OB 的中垂线上,过D作DH⊥OB,垂足是H 则H 是OB 中点。DH=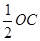
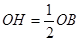 ∴D
∴D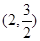
2) BD=BO 过D作DG⊥OB,垂足是G ∴OG:OB=CD:CB DG:OC=1:5
∴ OG:4=1:5 DG:3=1:5 ∴OG=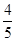 DG=
DG=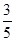 ∴D(
∴D(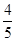 ,
,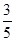 )
)
【解析】略

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.
 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.
 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.