题目内容
【题目】分析探索题：细心观察如图，认真分析各式，然后解答问题．
OA22=（
）2+1=2 S1=
；
OA32=（
）2+1=3 S2=
；
OA42=（
）2+1=4 S3=
…
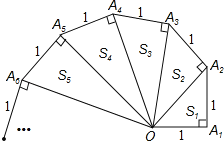
（1）请用含有n（n为正整数）的等式Sn= ；
（2）推算出OA10= ．
（3）求出 S12+S22+S32+…+S102的值．
【答案】（1）
（n是正整数）；（2）
；（3）
.
【解析】
试题分析：（1）此题要利用直角三角形的面积公式，观察上述结论，会发现，第n个图形的一直角边就是
，然后利用面积公式可得．
（2）由同述OA2=
，0A3=
…可知OA10=
．
（3）S12+S22+S32+…+S102的值就是把面积的平方相加就可．
试题解析：（1）（）2+1=n+1
Sn=（n是正整数）；
（2）∵OA12=1，
OA22=（
）2+1=2，
OA32=（）2+1=3，
OA42=（）2+1=4，
∴OA1=，
OA2=，
OA3=，…
∴OA10=；
（3）S12+S22+S32+…+S102
=（
）2+（
）2+（
）2+…+（
）2
=
（1+2+3+…+10）
=．
即：S12+S22+S32+…+S102=．
练习册系列答案
相关题目
【题目】某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共8台，具体情况如下表：
A型 | B型 | |
价格（万元/台） | 12 | 10 |
月污水处理能力（吨/月） | 200 | 160 |
经预算，企业最多支出89万元购买设备，且要求月处理污水能力不低于1380吨．
（1）该企业有几种购买方案？
（2）哪种方案更省钱，说明理由．
