题目内容
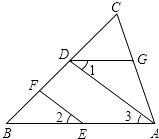
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;
⑤∠BDC= ![]() ∠BAC.
∠BAC.
其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个
【答案】B
【解析】解答:由三角形的外角性质得,∠EAC=∠ABC+∠ACB=2∠ABC,∵AD是∠EAC的平分线,∴∠EAC=2∠EAD,∴∠EAD=∠ABC,∴AD∥BC,故①正确;
∵AD∥BC,∴∠ADB=∠CBD,∵BD平分∠ABC,∴∠ABC=2∠CBD,∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,故②正确;
∵AD∥BC,∴∠ADC=∠DCF,∵CD是∠ACF的平分线,∴∠ADC= ![]() ∠ACF=
∠ACF= ![]() (180°-∠ACB)=
(180°-∠ACB)= ![]() (180°-∠ABC)=90°-∠ABD,故③正确;
(180°-∠ABC)=90°-∠ABD,故③正确;
由三角形的外角性质得,∠ACF=∠ABC+∠BAC,∠DCF=∠BDC+∠DBC,
∵BD平分∠ABC,CD平分∠ACF,
∴∠DBC= ![]() ∠ABC,∠DCF=
∠ABC,∠DCF= ![]() ∠ACF,
∠ACF,
∴∠DBC +∠BDC = ![]() ∠ACF=
∠ACF= ![]() (∠ABC+∠BAC)=
(∠ABC+∠BAC)= ![]() ∠ABC+
∠ABC+ ![]() ∠BAC=∠DBC+
∠BAC=∠DBC+ ![]() ∠BAC,
∠BAC,
∴∠BDC= ![]() ∠BAC,故⑤正确;
∠BAC,故⑤正确;
∵AD∥BC,
∴∠CBD=∠ADB,
∵∠ABC与∠BAC不一定相等,
∴∠ADB与∠BDC不一定相等,
∴BD平分∠ADC不一定成立,故④错误;
综上所述,结论正确的是①②③⑤共4个.
分析:此本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,三角形的内角和定理,平行线的判定与性质,熟记各性质并综合分析,理清图中各角度之间的关系是解题的关键.
【考点精析】本题主要考查了三角形的外角的相关知识点,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案