题目内容
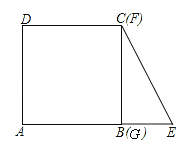
【题目】已知:在平面直角坐标系中,点O为坐标原点,直线y=﹣![]() x+b与x轴交于点A,与y轴交于点C.经过点A,C的抛物线y=ax2+3ax﹣3与x轴的另一个交点为点B.
x+b与x轴交于点A,与y轴交于点C.经过点A,C的抛物线y=ax2+3ax﹣3与x轴的另一个交点为点B.
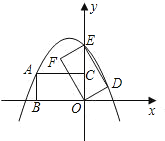
(1)如图1,求a的值;
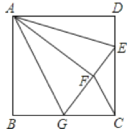
(2)如图2,点D,E分别在线段AC,AB上,且BE=2AD,连接DE,将线段DE绕点D顺时针旋转得到线段DF,且旋转角∠EDF=∠OAC,连接CF,求tan∠ACF的值;
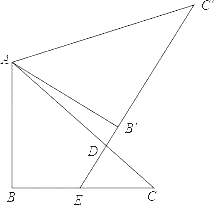
(3)如图3,在(2)的条件下,当∠DFC=135°时,在线段AC的延长线上取点M,过点M作MN∥DE交抛物线于点N,连接DN,EM,若MN=DF,求点N的横坐标.
【答案】(1)a=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)求出点A(﹣4,0),将点A的坐标代入二次函数表达式,即可求解;
(2)证明△ADE≌△GFD,即可求解;
(3)证明△DET≌△MSN(AAS),则MS=DT=![]() ,NS=ET=
,NS=ET=![]() ,设点M(x,﹣
,设点M(x,﹣![]() x﹣3),则点N(x﹣
x﹣3),则点N(x﹣![]() ,
,![]() ),将点N的坐标代入二次函数表达式,即可求解.
),将点N的坐标代入二次函数表达式,即可求解.
解:(1)y=ax2+3ax﹣3,当x=0,y=﹣3,故点C(0,﹣3),
将点C的坐标代入直线表达式并解得:b=﹣3,
则直线AC的表达式为:y=﹣![]() x﹣3,则点A(﹣4,0),
x﹣3,则点A(﹣4,0),
将点A的坐标代入二次函数表达式并解得:a=![]() ;
;
(2)在直线AC上取点G使DG=AE,连接FG,过点F作FH⊥AC,
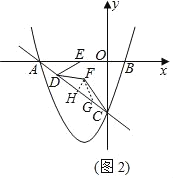
∵∠FDC+∠FDE=∠BAC+∠AED,而∠BAC=∠EDF,
∴∠FDH=∠AED,
而DG=AE,DF=DE,
∴△ADE≌△GFD,
∴AD=GF,
∵AB=AC=5,BE=2AD,
∴AD=GF=CG,
∵tan∠BAC=![]() ,设FH=3m,则HG=4m,FG=5m=GC,
,设FH=3m,则HG=4m,FG=5m=GC,
tan∠ACF=![]() ;
;
(3)如图3,过点D作DR⊥FC交FC的延长线于点R,过点F作FH⊥CD交于点H,
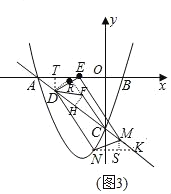
由(2)知tan∠ACF=![]() ,
,
在Rt△CDR中,设DR=![]() t,则CR=3
t,则CR=3![]() t,CD=10t,
t,CD=10t,
∵∠DFC=135°,则△DFR是等腰直角三角形,则FR=DR=![]() t,
t,
CF=CR﹣CF=2![]() t,
t,
在Rt△FHC中,tan∠ACF=![]() ,
,
则FH=2t,CH=6t,DH=CD﹣CH=10t﹣6t=4t,
则tan∠FDH=![]() =tan∠AED,
=tan∠AED,
在Rt△ADT中,tan∠BAC=![]() ,
,
设:DT=3n,则AT=4n,AD=5n,
在Rt△DTE中,tan∠AED=![]() ,
,
则ET=2DT=6n,BE=2AD=10n,
∵AT+TE+BE=AB,即4n+6n+10n=5,
解得:n=![]() ,
,
则ET=![]() ,DT=
,DT=![]() ;
;
∵MN=EF=DE,且MN∥DE,
∴四边形MNDE为平行四边形,∴∠DEM=∠DNM,
过点N作x轴的平行线交直线AC于点K,过点M作MS⊥NK于点S,
则∠AEM=∠KND,∴∠TED=∠MNS,
而MN=DE,∠ETD=∠MSN=90°,
∴△DET≌△MSN(AAS),
∴MS=DT=![]() ,NS=ET=
,NS=ET=![]() ,
,
设点M(x,﹣![]() x﹣3),则点N(x﹣
x﹣3),则点N(x﹣![]() ,
,![]() ),
),
将点N的坐标代入二次函数表达式得:
![]()
解得:![]() (舍去负值),
(舍去负值),
故点N的横坐标为:![]() .
.

 精英口算卡系列答案
精英口算卡系列答案